练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．计算：（-45）÷[（-$\frac{1}{3}$）÷（-$\frac{2}{5}$）]．

    分析 首先根据有理数的除法法则，求出（-$\frac{1}{3}$）÷（-$\frac{2}{5}$）的值是多少；然后用-45除以所得的商，求出算式（-45）÷[（-$\frac{1}{3}$）÷（-$\frac{2}{5}$）]的值是多少即可．

    解答 解：（-45）÷[（-$\frac{1}{3}$）÷（-$\frac{2}{5}$）]
    =（-45）÷$\frac{5}{6}$
    =-54．

    点评 此题主要考查了有理数的除法，要熟练掌握，解答此题的关键是要熟练掌握有理数的除法法则．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    5．下列各式从左至右的变形中，一定正确的是（　　）
    A．$\sqrt{ab}$=$\sqrt{a}$•$\sqrt{b}$B．$\sqrt{{a}^{2}}$=aC．$\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$D．$\sqrt{\frac{x}{y}}$=$\frac{\sqrt{x}}{\sqrt{y}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．x与$\frac{2}{3}$的差的一半是正数，用不等式表示为（　　）
    A．$\frac{1}{2}$（x-$\frac{2}{3}$）＞0B．$\frac{1}{2}$x-$\frac{2}{3}$＜0C．$\frac{1}{2}$x-$\frac{2}{3}$＞0D．$\frac{1}{2}$（x-$\frac{2}{3}$）＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

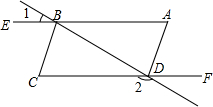    3．如图，AE∥CF，∠A=∠C．
    （1）若∠1=35°，求∠2的度数；
    （2）判断AD与BC的位置关系，并说明理由；
    （3）若AD平分∠BDF，试说明BC平分∠DBE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．⊙O过点B，C，圆心O在等腰直角△ABC内部，∠BAC=90°，OA=1，BC=6，则⊙O的半径为（　　）
    A．$\sqrt{10}$B．2$\sqrt{3}$C．$\sqrt{13}$D．3$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷（解析版） 题型：解答题

    小明受《乌鸦喝水》故事的启发，利用量筒和体积相同的小球进行了如下操作：

    请根据图中给出的信息，解答下列问题：

    （1）放入一个小球量筒中水面升高_______cm；

    （2）求放入小球后量筒中水面的高度y（cm）与小球个数x（个）之间的一次函数关系式（不要求写出自变量的取值范围）；

    （3）量筒中至少放入几个小球时有水溢出？

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷（解析版） 题型：填空题

    给定一列分式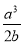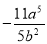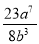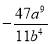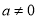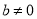： 、、、、……（， ），则第五个分式是__________________ ，第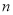个分式是__________________ ；

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年陕西省咸阳市七年级下学期第一次月考数学试卷（解析版） 题型：解答题

    认真阅读材料，然后回答问题：我们初中学习了多项式的运算法则，相应的我们可以计算出多项式的展开式，如：（a+b）1=a+b，

    （a+b）2=a2+2ab+b2，（a+b）3=a3+3a2b+3ab2+b3，…下面我们依次对（a+b）n展开式的各项系数进一步研究发现，当n取正整数是可以单独列成表中的形式：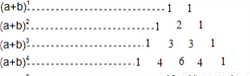

    上面的多项式展开系数表称为“杨辉三角形”；仔细观察“杨辉三角形”，用你发现的规律回答下列问题：（1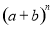）展开式中共有多少项？

    （2）请写出多项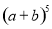式的展开式？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

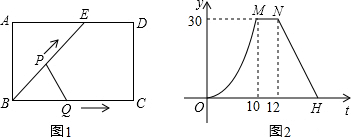    14．如图1，点E为矩形ABCD的边AD上一点，点P、点Q同时从点B出发，点P沿BE→ED→DC 运动到点C停止，点Q沿BC运动到点C停止，它们运动的速度都是1cm/s，设P、Q出发t秒时，△BPQ的面积为ycm2，已知y与t的函数关系如图2（曲线OM为抛物线的一部分），则下列结论：
    ①AB=6cm；
    ②当0＜t≤10时，y=$\frac{3}{10}$t2；
    ③NH所在直线的解析式为y=-5t+90；
    ④sin∠PBQ=$\frac{1}{2}$时，t=13秒．
    其中错误的结论个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    同步练习册答案