【题目】如图，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB的度数．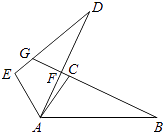 
科目：初中数学 来源： 题型：
【题目】如图1所示，在A，B两地之间有汽车站C站，客车由A地驶往C站，货车由B地驶往A地．两车同时出发，匀速行驶．图2是客车、货车离C站的路程y1 ， y2（千米）与行驶时间x（小时）之间的函数关系图象．
（1）填空：A，B两地相距千米；
（2）求两小时后，货车离C站的路程y2与行驶时间x之间的函数关系式；
（3）客、货两车何时相遇？相遇处离C站的路程是多少千米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在平面直角坐标系中，第一象限内长方形ABCD，AB∥y轴，点A（1，1），点C（a，b），满足
+|b﹣3|=0．
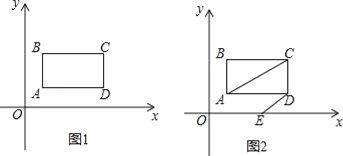
（1）求长方形ABCD的面积．
（2）如图2，长方形ABCD以每秒1个单位长度的速度向右平移，同时点E从原点O出发沿x轴以每秒2个单位长度的速度向右运动，设运动时间为t秒．
①当t=4时，直接写出三角形OAC的面积为 ；
②若AC∥ED，求t的值；
（3）在平面直角坐标系中，对于点P（x，y），我们把点P′（﹣y+1，x+1）叫做点P的伴随点，已知点A1的伴随点为A2，点A2的伴随点为A3，点A3的伴随点为A4，…，这样依次得到点A1，A2，A3，…，An．
①若点A1的坐标为（3，1），则点A3的坐标为 ，点A2014的坐标为 ；
②若点A1的坐标为（a，b），对于任意的正整数n，点An均在x轴上方，则a，b应满足的条件为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司准备投资开发A、B两种新产品，信息部通过调研得到两条信息：
信息一：如果投资A种产品，所获利润
（万元）与投资金额x（万元）之间满足正比例函数关系： 
；
信息二：如果投资B种产品，所获利润
（万元）与投资金额x（万元）之间满足二次函数关系： 
；
根据公司信息部报告， 
、
（万元）与投资金额x（万元）的部分对应值如下表所示：
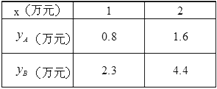
（1）填空： 
= ； 
= ；
（2）如果公司准备投资20万元同时开发A、B两种新产品，设公司所获得的总利润为W（万元），B种产品的投资金额为x（万元），则A种产品的投资金额为_________万元，并求出W与x之间的函数关系式；
（3）请你设计一个在（2）中公司能获得最大总利润的投资方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙、丙三位歌手进入“我是歌手”的冠、亚、季军的决赛，他们通过抽签来决定演唱顺序．
（1）求甲第一位出场的概率；
（2）求甲比乙先出场的概率．请用列表法或画树状图进行分析说明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题背景:
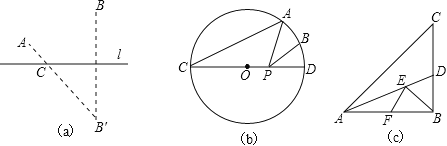
如图（a）,点A、B在直线l的同侧，要在直线l上找一点C，使AC与BC的距离之和最小，我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C，则点C即为所求.
（1）实践运用：
如图(b)，已知，⊙O的直径CD为4，点A 在⊙O 上，∠ACD=30°，B 为弧AD 的中点，P为直径CD上一动点，则BP+AP的最小值为 ．
（2）知识拓展：
如图(c)，在Rt△ABC中，AB=10，∠BAC=45°，∠BAC的平分线交BC于点D，E、F分别是线段AD和AB上的动点，求BE+EF的最小值，并写出解答过程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
