
【题目】问题背景:
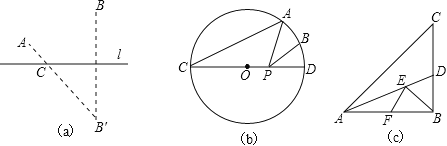
如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C,则点C即为所求.
(1)实践运用:
如图(b),已知,⊙O的直径CD为4,点A 在⊙O 上,∠ACD=30°,B 为弧AD 的中点,P为直径CD上一动点,则BP+AP的最小值为 .
(2)知识拓展:
如图(c),在Rt△ABC中,AB=10,∠BAC=45°,∠BAC的平分线交BC于点D,E、F分别是线段AD和AB上的动点,求BE+EF的最小值,并写出解答过程.
【答案】解:(1)![]() 。
。
(2)如图,在斜边AC上截取AB′=AB,连接BB′。
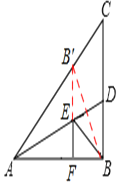
∵AD平分∠BAC,∴点B与点B′关于直线AD对称。
过点B′作B′F⊥AB,垂足为F,交AD于E,连接BE。
则线段B′F的长即为所求 (点到直线的距离最短) 。
在Rt△AFB/中,∵∠BAC=450, AB/="AB=" 10,
∴![]() 。
。
∴BE+EF的最小值为![]()
【解析】试题分析:(1)找点A或点B关于CD的对称点,再连接其中一点的对称点和另一点,和MN的交点P就是所求作的位置,根据题意先求出∠C′AE,再根据勾股定理求出AE,即可得出PA+PB的最小值:
如图作点B关于CD的对称点E,连接AE交CD于点P,此时PA+PB最小,且等于A。作直径AC′,连接C′E,
根据垂径定理得弧BD=弧DE。
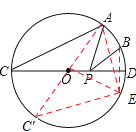
∵∠ACD=30°,∴∠AOD=60°,∠DOE=30°。∴∠AOE=90°。
∴∠C′AE=45°。
又AC为圆的直径,∴∠AEC′=90°。
∴∠C′=∠C′AE=45°。∴C′E=AE=![]() AC′=
AC′=![]() 。
。
∴AP+BP的最小值是![]() 。
。
(2)首先在斜边AC上截取AB′=AB,连接BB′,再过点B′作B′F⊥AB,垂足为F,交AD于E,连接BE,则线段B′F的长即为所求。


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,真命题的个数是( )
①过一点有且只有一条直线与已知直线平行;
②过一点有且只有一条直线与已知直线垂直;
③图形平移的方向一定是水平的;
④内错角相等.
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90。 , AC<BC,D为AB的中点,DE交AC于点E,DF交BC于点F,且DE⊥DF,过点A作AG//BC交FD的延长线于点G.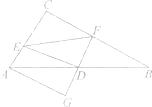
(1)求证:AG=BF;
(2)若AE=4,BF=8,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中
①无理数都是无限小数;
② ![]() 的平方根是±4;
的平方根是±4;
③无理数与数轴上的点一一对应;
④﹣ ![]() <﹣
<﹣ ![]() ;
;
正确的语句个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“汉字听写”比赛,每位学生听写汉字![]() 个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
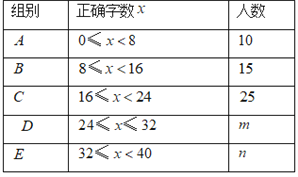


根据以上信息解决下列问题:
(![]() )在统计表中,
)在统计表中,![]() __________,
__________,![]() __________,并补全条形统计图.
__________,并补全条形统计图.
(![]() )扇形统计图中“
)扇形统计图中“![]() 组”所对应的圆心角的度数是__________.
组”所对应的圆心角的度数是__________.
(![]() )若该校共有
)若该校共有![]() 名学生,如果听写正确的个数少于
名学生,如果听写正确的个数少于![]() 个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com