
分析 先根据等式性质,得出[$\frac{a}{(b-c)^{2}}$+$\frac{b}{(c-a)^{2}}$+$\frac{c}{(a-b)^{2}}$]+$\frac{{a}^{2}-{a}^{2}+{b}^{2}-{b}^{2}+{c}^{2}-{c}^{2}}{(a-b)(b-c)(c-a)}$=0,再将添加的部分进行拆分,并约分化简,即可得到[$\frac{a}{(b-c)^{2}}$+$\frac{b}{(c-a)^{2}}$+$\frac{c}{(a-b)^{2}}$]+$\frac{a+b}{(b-c)(c-a)}$+$\frac{b+c}{(c-a)(a-b)}$+$\frac{c+a}{(a-b)(b-c)}$=0,左边因式分解即可得到[$\frac{a}{b-c}$+$\frac{b}{c-a}$+$\frac{c}{a-b}$][$\frac{1}{b-c}$+$\frac{1}{c-a}$+$\frac{1}{a-b}$]=0,进而得出$\frac{a}{b-c}$+$\frac{b}{c-a}$+$\frac{c}{a-b}$=0.
解答 解:∵$\frac{a}{(b-c)^{2}}$+$\frac{b}{(c-a)^{2}}$+$\frac{c}{(a-b)^{2}}$=0,
∴[$\frac{a}{(b-c)^{2}}$+$\frac{b}{(c-a)^{2}}$+$\frac{c}{(a-b)^{2}}$]+$\frac{{a}^{2}-{a}^{2}+{b}^{2}-{b}^{2}+{c}^{2}-{c}^{2}}{(a-b)(b-c)(c-a)}$=0,
∴[$\frac{a}{(b-c)^{2}}$+$\frac{b}{(c-a)^{2}}$+$\frac{c}{(a-b)^{2}}$]+$\frac{{a}^{2}-{b}^{2}}{(a-b)(b-c)(c-a)}$+$\frac{{b}^{2}-{c}^{2}}{(a-b)(b-c)(c-a)}$+$\frac{{c}^{2}-{a}^{2}}{(a-b)(b-c)(c-a)}$=0,
∴[$\frac{a}{(b-c)^{2}}$+$\frac{b}{(c-a)^{2}}$+$\frac{c}{(a-b)^{2}}$]+$\frac{a+b}{(b-c)(c-a)}$+$\frac{b+c}{(c-a)(a-b)}$+$\frac{c+a}{(a-b)(b-c)}$=0,
∴[$\frac{a}{b-c}$+$\frac{b}{c-a}$+$\frac{c}{a-b}$][$\frac{1}{b-c}$+$\frac{1}{c-a}$+$\frac{1}{a-b}$]=0,
∴[$\frac{a}{b-c}$+$\frac{b}{c-a}$+$\frac{c}{a-b}$]•$\frac{ac+bc+ab-{a}^{2}-{b}^{2}-{c}^{2}}{(a-b)(b-c)(c-a)}$=0,
又∵ac+bc+ab-a2-b2-c2=-$\frac{1}{2}$[(a-c)2+(b-c)2+(a-b)2]≠0,
∴$\frac{ac+bc+ab-{a}^{2}-{b}^{2}-{c}^{2}}{(a-b)(b-c)(c-a)}$≠0,
∴$\frac{a}{b-c}$+$\frac{b}{c-a}$+$\frac{c}{a-b}$=0.
点评 本题主要考查了分式的化简求值,解决问题的关键是配方法的运用,在化简的过程中要注意运算顺序,化简的最后结果分子、分母要进行约分,结果要化成最简分式或整式.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB=a,P是线段AB上一点,分别以AP、BP为边作正方形.
如图,AB=a,P是线段AB上一点,分别以AP、BP为边作正方形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
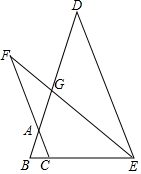 如图,在△ABC中,AB=AC,点D、E、F为三边延长线上的点,且DE∥AC,连接EF交BD于点G,∠BEF+2∠B=180°.
如图,在△ABC中,AB=AC,点D、E、F为三边延长线上的点,且DE∥AC,连接EF交BD于点G,∠BEF+2∠B=180°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com