
分析 ①已知点B在抛物线E上,将该点坐标代入抛物线E的解析式中直接求解,即可得到n的值.
②将点A的坐标代入抛物线E上直接进行验证即可;
③代入t=2得到二次函数,从而确定其增减性即可.
④将t的值代入“再生二次函数”中,通过配方可得到顶点的坐标.
解答 解:①将x=-1代入抛物线E的解析式中,得:
n=t(x2-3x+2)+(1-t)(-2x+4)=6,正确.
②将x=2代入y=t(x2-3x+2)+(1-t)(-2x+4),得 y=0,
∴点A(2,0)在抛物线E上,正确.
③当t=2时,y=t(x2-3x+2)+(1-t)(-2x+4)=2x2-4x=2(x-1)2-2,
对称轴为x=1,开口向上,
∴当x>2时,y随x的增大而增大,正确;
④将t=2代入抛物线E中,得:y=t(x2-3x+2)+(1-t)(-2x+4)=2x2-4x=2(x-1)2-2,
∴此时抛物线的顶点坐标为:(1,-2),错误;
故答案为:①②③
点评 此题考查了二次函数的性质知识,该题通过新定义的形式考查了二次函数等综合知识,理解新名词的含义尤为关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
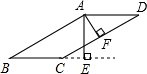 如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,点E,F为垂足,∠EAF=30°,AE=3cm,AF=2cm,求平行四边形ABCD的周长.
如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,点E,F为垂足,∠EAF=30°,AE=3cm,AF=2cm,求平行四边形ABCD的周长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
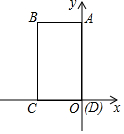 如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(-6,8),C(-6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为(-6,4),(-6,2$\sqrt{7}$),(-6,8-2$\sqrt{7}$).
如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(-6,8),C(-6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为(-6,4),(-6,2$\sqrt{7}$),(-6,8-2$\sqrt{7}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com