
分析 (1)根据幂的乘方、有理数的乘法和加减法可以解答本题;
(2)根据分式的减法和分式的除法可以解答本题.
解答 解:(1)(-1)3-($\frac{1}{3}$)-2×$\frac{2}{9}$+6×|-$\frac{2}{3}$|
=(-1)-9×$\frac{2}{9}+6×\frac{2}{3}$
=(-1)-2+4
=1;
(2)($\frac{1}{a+b}$$-\frac{1}{a-b}$)÷$\frac{b}{{a}^{2}-2ab+{b}^{2}}$
=$\frac{(a-b)-(a+b)}{(a+b)(a-b)}×\frac{(a-b)^{2}}{b}$
=$\frac{-2b}{(a+b)(a-b)}×\frac{(a-b)^{2}}{b}$
=$-\frac{2a-2b}{a+b}$,
当a=1,b=2时,原式=$-\frac{2×1-2×2}{1+2}=\frac{2}{3}$.
点评 本题考查分式的化简求值、负整数指数幂,解答本题的关键是明确分式化简求值的方法.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:解答题
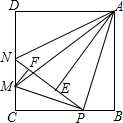 如图,在正方形ABCD中,AB=4,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处,在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.
如图,在正方形ABCD中,AB=4,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处,在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
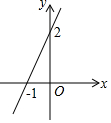 如图所示是一次函数y=kx+b在直角坐标系中的图象,通过观察图象我们就可以得到方程kx+b=0的解为x=-1,这一求解过程主要体现的数学思想是( )
如图所示是一次函数y=kx+b在直角坐标系中的图象,通过观察图象我们就可以得到方程kx+b=0的解为x=-1,这一求解过程主要体现的数学思想是( )| A. | 数形结合 | B. | 分类讨论 | C. | 类比 | D. | 公理化 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,点P是BC边上一点(不与B、C重合),连接PA,将线段PA绕点P顺时针旋转90°得到线段PE,交边DC于F,连接AE,CE.
如图,在正方形ABCD中,点P是BC边上一点(不与B、C重合),连接PA,将线段PA绕点P顺时针旋转90°得到线段PE,交边DC于F,连接AE,CE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com