
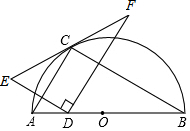
 如图,点C在以AB为直径的半圆上,AB=4$\sqrt{5}$,AC=4,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是32.
如图,点C在以AB为直径的半圆上,AB=4$\sqrt{5}$,AC=4,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是32.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{10}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
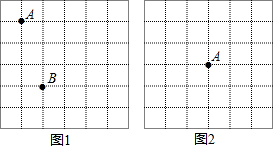
 如图,E,F,G,H分别是边BD、BC、AC、AD的中点,且AB=CD=6,现有下列结论:①EG⊥FH;②四边形EFGH是矩形;③HF平分∠EHG;④四边形EFGH的周长是12.其中正确的是①③④.(把所有正确结论的序号都选上)
如图,E,F,G,H分别是边BD、BC、AC、AD的中点,且AB=CD=6,现有下列结论:①EG⊥FH;②四边形EFGH是矩形;③HF平分∠EHG;④四边形EFGH的周长是12.其中正确的是①③④.(把所有正确结论的序号都选上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
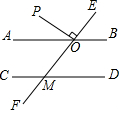 如图,已知直线AB∥CD,直线EF分别与AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为点O,若∠AOP=30°,求∠EMD的度数.
如图,已知直线AB∥CD,直线EF分别与AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为点O,若∠AOP=30°,求∠EMD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  黑桃Q | B. |  梅花2 | C. |  梅花6 | D. |  方块9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com