
【题目】已知二次函数![]() .
.
(1)用配方法求出函数的顶点坐标;
(2)求出该二次函数图象与![]() 轴的交点坐标。
轴的交点坐标。
(3)该图象向右平移 个单位,可使平移后所得图象经过坐标原点.请直接写出平移后所得图象与![]() 轴的另一个交点的坐标为 .
轴的另一个交点的坐标为 .
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
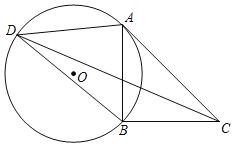
【题目】如图,线段AB为⊙O的一条弦,以AB为直角边作等腰直角△ABC,直线AC恰好是⊙O的切线,点D为⊙O上的一点,连接DA,DB,DC,若DA=3,DB=4,则DC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
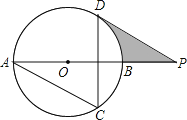
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李师傅驾驶出租车匀速地从西安市送客到咸阳国际机场,全程约![]() ,设小汽车的行驶时间为
,设小汽车的行驶时间为![]() (单位:
(单位:![]() ),行驶速度为
),行驶速度为![]() (单位:
(单位:![]() ),且全程速度限定为不超过
),且全程速度限定为不超过![]() .
.
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)李师傅上午![]() 点驾驶小汽车从西安市出发.需在
点驾驶小汽车从西安市出发.需在![]() 分钟后将乘客送达咸阳国际机场,求小汽车行驶速度
分钟后将乘客送达咸阳国际机场,求小汽车行驶速度![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降价x元,商场一天可通过A商品获利润y元.
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)
(2)A商品销售单价为多少时,该商场每天通过A商品所获的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
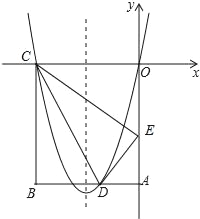
【题目】如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求点E坐标及经过O,D,C三点的抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(2)中的抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
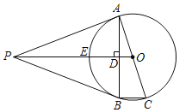
【题目】如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)求证:E为△PAB的内心;
(3)若cos∠PAB=![]() ,BC=1,求PO的长.
,BC=1,求PO的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com