
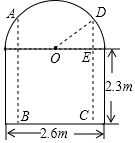
 一辆装货的小货车高2.9m,宽为2.4m.要开进下部为长方形,上部为半圆形的某仓库大门(如图),这辆货车能否通过大门?请说明理由.
一辆装货的小货车高2.9m,宽为2.4m.要开进下部为长方形,上部为半圆形的某仓库大门(如图),这辆货车能否通过大门?请说明理由. 科目:初中数学 来源: 题型:选择题
 如图,直线1表示铁路,A、B两点表示某工厂两个生产区,若要在铁路旁修建一个货仓C,使货仓C到两个生产区A,B的距离之和最短,则这样的点C的位置( )
如图,直线1表示铁路,A、B两点表示某工厂两个生产区,若要在铁路旁修建一个货仓C,使货仓C到两个生产区A,B的距离之和最短,则这样的点C的位置( )| A. | 有1处 | B. | 有2处 | C. | 有4处 | D. | 不存在 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
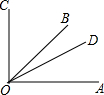 如图,已知∠COA=90°,∠COD比∠DOA大n°,且OB是∠COA的平分线.
如图,已知∠COA=90°,∠COD比∠DOA大n°,且OB是∠COA的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{15}{4}$ | B. | $\frac{15}{2}$ | C. | 4 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
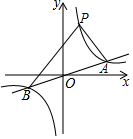 如图,反比例函数y=$\frac{k}{x}$与y=mx交于A、B两点,已知点A的坐标是(4,2),点P是第一象限内反比例函数图象上的动点,且在AB的上方.
如图,反比例函数y=$\frac{k}{x}$与y=mx交于A、B两点,已知点A的坐标是(4,2),点P是第一象限内反比例函数图象上的动点,且在AB的上方.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com