
| 销售方式 | 批发 | 零售 | 加工销售 |
| 利润(百元/吨) | 12 | 20 | 28 |
分析 (1)由加工量仅为批发量的一半可得出加工量为$\frac{x}{2}$吨,再依据生产基地收获柑橘40吨得出零售量,根据题意列出方程即可,假设零售量为0,即能找出x的取值范围;
(2)由零售量不超过批发量找出x的取值范围,根据一次函数的单调性,即可求出最大利润.
解答 解:(1)∵加工量仅为批发量的一半,
∴加工量为$\frac{x}{2}$吨,零售量为40-x-$\frac{x}{2}$吨.
根据题意,有y=12x+20×(40-x-$\frac{x}{2}$)+28×$\frac{x}{2}$=800-4x.
令零售量=0,即40-x-$\frac{x}{2}$=0,解得:x=$\frac{80}{3}$.
故y与x之间的函数关系式为y=-4x+800(0≤x≤$\frac{80}{3}$).
(2)∵零售量不超过批发量,
∴有40-x-$\frac{x}{2}$≤x,解得:x≥16.
∵总利润为y百元与批发量x吨之间的关系式为y=-4x+800,单调递减,
∴当x=16时,总利润最大,此时y=-4×16+800=736.
答:该生产基地按计划全部售完柑橘后获得的最大利润为736百元.
点评 本题考查了一次函数的应用中的求极值问题,解题的关键:(1)找出x的取值范围;(2)结合函数的单调性求极值.本题属于中档偏易题,主要失分点在于(1)忘记加上x的取值范围;(2)重新界定x的取值范围.解决该类问题的最好办法是,多读几遍题,弄懂题意,找到入手点再做.


科目:初中数学 来源: 题型:解答题
 甲、乙两人玩如图所示的转盘游戏,游戏规则是:转盘被平均分作3个区域,颜色分别为黑、白、红,转动转盘时,指针指向的颜色,即为转出的颜色,如果指针指在两区域之间,则重转一次.两人参与游戏,一人转动两次转盘,另一人猜颜色,若转出的颜色与猜出的颜色所表示的特征相符,则猜颜色的人获胜;否则,转动转盘的人获胜.猜颜色的方法从下面三种方案中选一种.
甲、乙两人玩如图所示的转盘游戏,游戏规则是:转盘被平均分作3个区域,颜色分别为黑、白、红,转动转盘时,指针指向的颜色,即为转出的颜色,如果指针指在两区域之间,则重转一次.两人参与游戏,一人转动两次转盘,另一人猜颜色,若转出的颜色与猜出的颜色所表示的特征相符,则猜颜色的人获胜;否则,转动转盘的人获胜.猜颜色的方法从下面三种方案中选一种.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 车 型 运往地 | 甲 地(元/辆) | 乙 地(元/辆) |
| 大货车 | 720 | 800 |
| 小货车 | 500 | 650 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC的角平分线交AD于E,F在AE上,且AF=3,BE与CF交于点G,则△EFG与△BCG面积之比是$\frac{1}{16}$.
如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC的角平分线交AD于E,F在AE上,且AF=3,BE与CF交于点G,则△EFG与△BCG面积之比是$\frac{1}{16}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 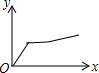 | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com