
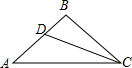
 如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )
如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:判断题
已知抛物线y=ax2+bx+c经过A(1,0)、B(5,0)两点,最高点纵坐标为4,与y轴交于点C.

(1)求抛物线的解析式;
(2)若△ABC的外接圆⊙O’交y轴于不同点C和D,⊙O’的弦DE平行于x轴,求直线CE的解析式;
(3)在x轴的负半轴上是否存在点F,使△OCF与△CDE相似?若存在求出符合条件的所有点F的坐标,并判定直线CF与⊙O’的位置关系;若不存在,请说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s.
如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-4\frac{2}{3}>-4.7$ | B. | $-\frac{12}{23}<-\frac{6}{11}$ | C. | -0.2<-0.22 | D. | $-0.01<-\frac{1}{100}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.2cm 0.3m 0.4cm 0.2cm | B. | 1cm 2cm 3cm 4cm | ||
| C. | 4cm 6cm 8cm 3cm | D. | $\sqrt{2}$cm $\sqrt{6}$cm $\sqrt{8}$cm $\sqrt{7}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 18 | B. | 12 | C. | 9 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com