练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知抛物线y=ax2+bx+c经过A(1,0)、B(5,0)两点，最高点纵坐标为4，与y轴交于点C．

    （1）求抛物线的解析式；

    （2）若△ABC的外接圆⊙O’交y轴于不同点C和D，⊙O’的弦DE平行于x轴，求直线CE的解析式；

    （3）在x轴的负半轴上是否存在点F，使△OCF与△CDE相似？若存在求出符合条件的所有点F的坐标，并判定直线CF与⊙O’的位置关系；若不存在，请说明理由？

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．一次函数y=-2x+3与y轴的交点坐标是（0，3），把直线y=-2x向上平移3个单位就得到y=-2x+3的图象；若向下平移5个单位就得到y=-2x-5的图象．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．已知一次函数y=kx+b，当x=1时，y=2，且它的图象与y轴交点的纵坐标是3，则此函数的表达式为y=-x+3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：
    （1）（5a+3b）（5a-3b）；
    （2）（1-mn）（mn+1）；
    （3）（-7x2y-3b2）（7x3y-3b2）；
    （4）（-$\frac{5}{6}$x-0.7y）（$\frac{5}{6}$x-0.7y）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：
    （1）2m2•（-2mn）•（-$\frac{1}{2}$m2n3）；
    （2）2x6y2•x3y+（-25x8y2）（-xy）

    查看答案和解析>>

    科目：初中数学 来源：2017届江苏省扬州市九年级下学期第一次月考数学试卷（解析版） 题型：判断题

    一张矩形纸片沿对角线剪开，得到两张三角形纸片，再将这两张三角形纸片摆成如下右图形式，使点B、F、C、D在同一条直线上．

    （1）求证AB⊥ED；

    （2）若PB=BC，请找出图中与此条件有关的一对全等三角形，并给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

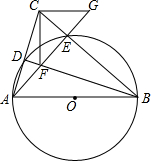    2．如图所示，△ABC中，AB是⊙O的直径，AC和BC分别和⊙O相交于点D和E，在BD上截取BF=AC，延长AE使AG=BC．求证：
    （1）CG=CF；
    （2）CG⊥CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

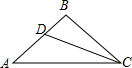    18．如图，在△ABC中，∠A=∠ACB，CD平分∠ACB交AB于点D，∠ADC=150°，则∠B为（　　）
    A．120°B．130°C．140°D．150°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，已知，抛物线y=ax2-2ax-3a与x轴交于A，B，与y轴负半轴交于C点，且OC=3OA．
    （1）求抛物线的解析式；
    （2）E为直线y=1上一动点，F为抛物线对称轴上一点，当F点在对称轴上何处时，四边形ACEF的周长最短？
    （3）点D（1，0）为x轴上一点，第四象限的抛物线上是否存在点P，使得线段AP与直线CD的夹角为45°？若存在这样的P点，请求出P点坐标，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案