
【题目】如图,AB是⊙O的直径,AC,BC分別与⊙O交于点D,E,则下列说法一定正确的是( )

A.连接BD,可知BD是△ABC的中线B.连接AE,可知AE是△ABC的高线
C.连接DE,可知![]() D.连接DE,可知S△CDE:S△ABC=DE:AB
D.连接DE,可知S△CDE:S△ABC=DE:AB
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】某商店经过市场调查,整理出某种商品在第![]() (
(![]() )天的售价与销量的相关信息如下表.已知该商品的进价为每件30元,设销售该商品每天的利润为
)天的售价与销量的相关信息如下表.已知该商品的进价为每件30元,设销售该商品每天的利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系是;
的函数关系是;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
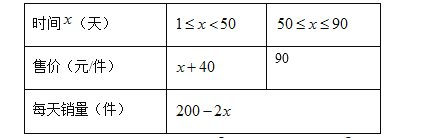
查看答案和解析>>
科目:初中数学 来源: 题型:
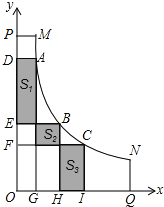
【题目】六一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A、B、C是弯道MN上的三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1、S2、S3,并测得S2=6(单位:平方米).OG=GH=HI.
(1)求S1和S3的值;
(2)设T(x,y)是弯道MN上的任一点,写出y关于x的函数关系式;
(3)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
查看答案和解析>>
科目:初中数学 来源: 题型:
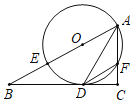
【题目】已知:△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)若DF∥AB,则BD与CD有怎样的数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,O为对角线AC的中点,点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,图中阴影部分面积的大小变化情况是( )

A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
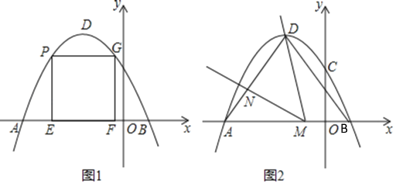
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c经过点A(﹣5,0)和点B(1,0).
x2+bx+c经过点A(﹣5,0)和点B(1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)点P是抛物线上A、D之间的一点,过点P作PE⊥x轴于点E,PG⊥y轴,交抛物线于点G,过点G作GF⊥x轴于点F,当矩形PEFG的周长最大时,求点P的横坐标;
(3)如图2,连接AD、BD,点M在线段AB上(不与A、B重合),作∠DMN=∠DBA,MN交线段AD于点N,是否存在这样点M,使得△DMN为等腰三角形?若存在,求出AN的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工人打算用不锈钢条加工一个面积为0.8平方米的矩形模具.假设模具的长与宽分别为x米和y米.
(1)你能写出y与x之间的函数解析式吗?
(2)变量y与x是什么函数关系?
(3)已知这种不锈钢条每米6元,若想使模具的长比宽多1.6米,则加工这个模具共需花多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com