
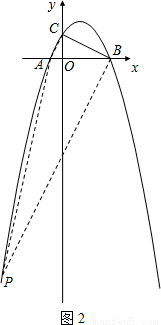
如图,二次函数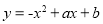 的图象与
的图象与 轴交于
轴交于 ,
, 两点,且与y轴交于点C.
两点,且与y轴交于点C.

(1)求该抛物线的关系式,并判断 的形状;
的形状;
(2)在x轴上方的抛物线上有一点D,且以A、B、C、D四点为顶点的四边形是等腰梯形,请直接写出D点的坐标 ;
(3)在此抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形是直角梯形?若存在,求出P点的坐标;若不存在,说明理由。
(1)抛物线的解析式为y=-x2+ x+1;△ABC是直角三角形,且∠ACB=90°(2)D(
x+1;△ABC是直角三角形,且∠ACB=90°(2)D( ,1);(3)点P(
,1);(3)点P( ,-
,- )或(-
)或(- ,-9)
,-9)
【解析】
试题分析:(1)将A、B的坐标代入抛物线的解析式中即可确定抛物线的解析式;进而可得到C点坐标,进而可求出AC、BC、AB的长,然后再判断△ABC的形状;
(2)根据抛物线和等腰梯形的对称性知,点C关于抛物线对称轴的对称点符合点D的要求,由此可求出点D的坐标;
(3)在(1)题已将证得∠ACB=90°,若A、C、B、P四点为顶点的四边形是直角梯形,则有两种情况需要考虑:
①以BC、AP为底,AC为高;可先求出直线BC的解析式,进而可确定直线AP的解析式,联立抛物线的解析式即可求出点P的坐标.
②以AC、BP为底,BC为高;方法同①.
试题解析:(1)由题意得: ,
,
解得 ;
;
∴抛物线的解析式为y=-x2+ x+1;
x+1;
∴C(0,1);
∴AC2= +1=
+1= ,BC2=1+4=5,AB2=(2+
,BC2=1+4=5,AB2=(2+ )2=
)2= ;
;
∴AC2+BC2=AB2,即△ABC是直角三角形,且∠ACB=90°
(2)由(1)的抛物线知:其对称轴方程为x= ;
;
根据抛物线和等腰梯形的对称性知:点D( ,1);
,1);

(3)存在,点P( ,-
,- )或(-
)或(- ,-9);
,-9);
若以A、C、B、P四点为顶点的直角梯形以BC、AP为底;
∵B(2,0),C(0,1),
∴直线BC的解析式为:y=- x+1;
x+1;
设过点A且平行于BC的直线的解析式为y=- x+h,
x+h,
则有:(- )×(-
)×(- )+h=0,h=-
)+h=0,h=- ;
;
∴y=- x-
x- ;
;
联立抛物线的解析式有:

解得: 或
或
∴点P( ,
, );
);
若以A、C、B、P四点为顶点的直角梯形以AC、BP为底,
同理可求得P(- ,-9);
,-9);
故当P( ,
, )或(-
)或(- ,-9);时,以A、C、B、P四点为顶点的四边形是直角梯形.
,-9);时,以A、C、B、P四点为顶点的四边形是直角梯形.
(根据抛物线的对称性求出另一个P点坐标亦可)
考点:二次函数综合题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源:[同步]2014年人教版初中数学七年级下第十章10.3练习卷(解析版) 题型:选择题
(2013•青岛)一个不透明的口袋里装有除颜色外都相同的5个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小亮共摸了100次,其中有10次摸到白球.因此小亮估计口袋中的红球大约有( )个.
A.45 B.48 C.50 D.55
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC= ( )
| A.2:5 | B.2:3 | C.3:5 | D.3:2 |
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省九年级上学期第二次月考数学试卷(解析版) 题型:选择题
已知两圆的半径分别是5和8,若两圆相交,则两圆的圆心距可以是( )
A.3 B.8 C.13 D.18
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省九年级上学期第二次月考数学试卷(解析版) 题型:选择题
若抛物线 与y轴的交点为(0,
与y轴的交点为(0, )则该抛物线与x轴的交点是( )
)则该抛物线与x轴的交点是( )
A.(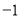 ,0)和(0,3) B.(0,
,0)和(0,3) B.(0,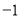 )和(3,0)
)和(3,0)
C.(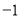 ,0)和(3,0) D.(0,
,0)和(3,0) D.(0,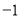 )和(0,3)
)和(0,3)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级上学期期末考试数学试卷(解析版) 题型:计算题
某中学开展“感恩父母”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示。
(1)根据下图,分别求出两班复赛的平均成绩和方差;

(2)根据(1)的计算结果,哪个班级的复赛成绩较好?为什么?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级上学期期末考试数学试卷(解析版) 题型:填空题
小张同学想用“描点法”画二次函数 的图象,取自变量x的5个值,请你指出这个算错的y值所对应的x= 。
的图象,取自变量x的5个值,请你指出这个算错的y值所对应的x= 。

查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省牡丹江管理局北斗星协会九年级中考三模数学试卷(解析版) 题型:解答题
(本小题满分8分)在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.

(1)在图1中请你通过观察、测量BF与CG的 长度,猜想并写出BF与CG满足的数量关系, 然后证明你的猜想;
(2)当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线上,另一条 直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG 的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;
(3)当三角尺在(2)的基础上沿AC方向继续平 移到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,(2)中的猜想是否 仍然成立?(不用说明理由)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省九年级上学期期末考试数学试卷(解析版) 题型:选择题
下列事件中的必然事件是( )
A.天气阴了之后下雨
B.小明上学路上看到两车相撞
C.抛掷一枚骰子,朝上的一面点数恰好是5
D.同时抛掷两枚骰子,朝上的两面点数之和小于13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com