【题目】如图，AD，BE分别是△ABC的中线和角平分线，AD⊥BE于点G，AD＝BE＝6，求AC的长．
考前必练系列答案科目：初中数学 来源： 题型：
【题目】计算：
(1)2－7＋5－3;
(2)－
－
＋
－
；
(3)(－40)－(＋27)＋19－24－(－32)；
(4)0.5－
＋
－－
；
(5)|－3.5|－
＋
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】规定：[x]表示不大于x的最大整数，（x）表示不小于x的最小整数，[x）表示最接近x的整数（x≠n+0.5，n为整数），例如：[2.3]=2，（2.3）=3，[2.3）=2．当﹣1＜x＜1时，化简 [x]+（x）+[x）的结果是__________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠BAP与∠APD互补，∠1＝∠2，试说明：∠E＝∠F.请在下面的括号中填上理由．
解：∵∠BAP与∠APD互补( )，
∴AB∥CD( )，
∴∠BAP＝∠APC( )．
又∵∠1＝∠2( )，
∴∠BAP－∠1＝∠APC－∠2( )，
即∠3＝∠4，
∴AE∥PF( )，
∴∠E＝∠F( )．
查看答案和解析>>
科目：初中数学 来源： 题型：
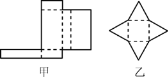
【题目】观察图，回答下列问题：
(1)甲、乙两图分别能折成什么几何体？简述它们的特征；
(2)设几何体的面数为F，顶点数为V，棱数为E，请计算(1)中两个几何体的F＋V－E的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等腰△ABC中，AB＝AC，BD，CE分别是边AC，AB上的中线，BD与CE相交于点O，点M，N分别为线段BO和CO的中点．求证：四边形EDNM是矩形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一次“构造勾股数”的探究性学习中，老师给出了下表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中
、
为正整数，且
．
（
）观察表格，当
， 
时，此时对应的
、
、
的值能否为直角三角形三边的长？说明你的理由．
（
）探究
， 
， 
与
、
之间的关系并用含
、
的代数式表示： 
__________， 
__________， 
__________．
（
）以
， 
， 
为边长的三角形是否一定为直角三角形？如果是，请说明理由；如果不是，请举出反例．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图A在数轴上所对应的数为﹣2．
（1）点B在点A右边距A点4个单位长度，求点B所对应的数；
（2）在（1）的条件下，点A以每秒2个单位长度沿数轴向左运动，点 B 以每秒2个单位长度沿数轴向右运动，当点A运动到﹣6所在的点处时，求A，B两点间距离．
（3）在（2）的条件下，现A点静止不动，B点再以每秒2个单位长度沿数轴向左运动时，经过多长时间A，B两点相距4个单位长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程解应用题．
程大位，明代商人，珠算发明家，被称为珠算之父、卷尺之父．少年时，读书极为广博，对数学颇感兴趣，60岁时完成其杰作《直指算法统宗》（简称《算法统宗》）．
在《算法统宗》里记载了一道趣题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完．试问大、小和尚各多少人？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
