
如图,点D,E在△ABC的边BC上,连 接AD,AE.①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①②?③:①③?②;②③?①.
(1)以上三个命题是真命题的为(直接作答) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明)

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源:2015届江苏无锡前洲中学八年级3月阶段练习数学试卷(解析版) 题型:解答题
如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
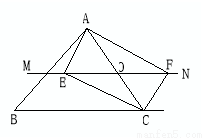
(1)求证:EO=FO;(3分)
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;(3分)
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论(4分)
查看答案和解析>>
科目:初中数学 来源:2015届江苏宜兴和桥学区八年级下学期期中考试数学试卷(解析版) 题型:选择题
如图,在□ABCD中,BD为对角线,E、F分别是AD、BD的中点,连结EF.若EF=3,则CD的长为( )
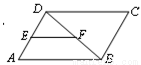
A.2 B.3 C.4 D.6
查看答案和解析>>
科目:初中数学 来源:2015届广东省深圳市石岩公学八年级3月质量检测数学试卷(解析版) 题型:选择题
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交B于点D,则下列说法中正确的个数是( )
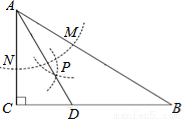
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2015届广东省深圳市石岩公学八年级3月质量检测数学试卷(解析版) 题型:选择题
若不等式(a-3)x>a-3的解集是x<1,则a的取值范围是( )
A.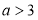 B.
B.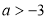 C.
C.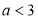 D.
D.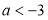
查看答案和解析>>
科目:初中数学 来源:2015届广东省云浮市八年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,△ABC中,∠1+∠2+∠3=_____度,∠4+∠5+∠6=_____度.
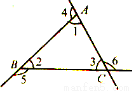
查看答案和解析>>
科目:初中数学 来源:2015届山西省孝义市八年级下学期期末考试数学试卷(解析版) 题型:解答题
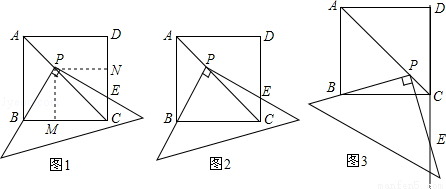
提出问题:如图1,将三角板放在正方形ABCD上,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交边DC与点E,求证:PB=PE
分析问题:学生甲:如图1,过点P作PM⊥BC,PN⊥CD,垂足分别为M,N通过证明两三角形全等,进而证明两条线段相等.
学生乙:连接DP,如图2,很容易证明PD=PB,然后再通过“等角对等边”证明PE=PD,就可以证明PB=PE了.
解决问题:请你选择上述一种方法给予证明.
问题延伸:如图3,移动三角板,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交DC的延长线于点E,PB=PE还成立吗?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com