
����Ŀ����֪�ڱ߳�Ϊ4������ABCD�У���EBF=��A=60�㣬
��1����ͼ�٣�����E��F�ֱ����߶�AD��DC�ϣ�
���жϡ�EBF����״����˵�����ɣ�
�����ı���ABFD�����Ϊ7![]() ����DE�ij���
����DE�ij���
��2����ͼ�ڣ�����E��F�ֱ����߶�AD��DC���ӳ����ϣ�BE��DC���ڵ�O�����BOF�����ΪS1����EOD�����ΪS2����S1-S2��ֵ�Ƿ�Ϊ��ֵ������ǣ��������ֵ��������ǣ���˵�����ɣ�
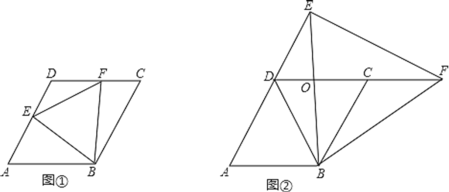
���𰸡���1���١�EBF�ǵȱ������Σ�����������DE=1����2��S1-S2��ֵ�Ƕ�ֵ��S1-S2=4![]() ��
��
��������
��1���١�EBF�ǵȱ������Σ�����BD��֤����ABE�ա�DBF��ASA�����ɽ�����⣮
����ͼ1�У���BH��AD��H�������ABE����������������ε������ʽ���AE���ɽ�����⣮
��2����ͼ2�У����ۣ�S1-S2��ֵ�Ƕ�ֵ����취֤����S1-S2=S��BCD���ɣ�
�⣺��1���١�EBF�ǵȱ������Σ��������£�
��ͼ1�У�����BD��
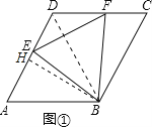
���ı���ABCD�����Σ�
��AD=AB��
�ߡ�ADB=60����
���ADB�ǵȱ������Σ���BDC�ǵȱ������Σ�
��AB=BD����ABD=��A=��BDC=60����
�ߡ�ABD=��EBF=60����
���ABE=��DBF��
����ABE����DBF��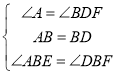 ��
��
���ABE�ա�DBF��ASA����
��BE=BF��
�ߡ�EBF=60����
���EBF�ǵȱ������Σ�
����ͼ1�У���BH��AD��H��
��Rt��ABH��BH=2![]() ��
��
��S��ABD=![]() ADBH=4
ADBH=4![]() ��
��
��S�ı���ABFD=7![]() ��
��
��S��BDF=S��ABE=3![]() ��
��
��![]() =3
=3![]() ��
��
��AE=3��
��DE=AD=AE=1��
��2����ͼ2�У����ۣ�S1-S2��ֵ�Ƕ�ֵ��
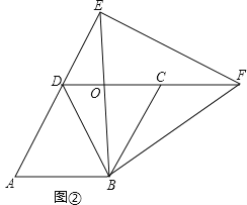
���ɣ��ߡ�BDC����EBF���ǵȱ������Σ�
��BD=BC����DBC=��EBF=60����BE=BF��
���DBE=��CBF��
���DBE�ա�CBF��SAS����
��S��BDE=S��BCF��
��S1-S2=S��BDE+S��BOC-S��DOE=S��DOE+S��BOD+S��BOC-S��DOE=S��BCD=![]() ��42=4
��42=4![]() ��
��
��S1-S2��ֵ�Ƕ�ֵ��


 Ŀ�����ϵ�д�
Ŀ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
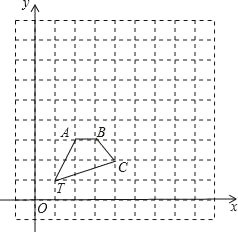
����Ŀ����ͼ���������������У��ı���TABC�Ķ�������ֱ�ΪT��1��1����A��2��3����B��3��3����C��4��2����
(1)�Ե�T��1��1��Ϊλ�����ģ���λ�����ĵ�ͬ�ཫ�ı���TABC�Ŵ�Ϊԭ����2�����Ŵ���A��B��C�Ķ�Ӧ��ֱ�ΪA�䣬B�䣬C�仭���ı���TA��B��C�䣻
(2)д����A�䣬B�䣬C������꣺
A���� ����B���� ����C���� ����
(3)��(1)�У���D��a��b��Ϊ�߶�AC����һ�㣬��仯���D�Ķ�Ӧ��D�������Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У��Գ���Ϊֱ��x=1��������y=��x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C���ҵ�B������Ϊ����1��0��
(1)�������ߵĽ���ʽ������ͼ��
(2)��D������Ϊ��0��1������P���������ϵĶ��㣬����PCD����CDΪ�ĵ��������Σ����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�ADƽ����BAC��BC�ڵ�D��AE��BC������ΪE����CF��AD��
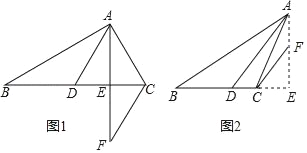
��1����ͼ1������ABC����������Σ���B=30�㣬��ACB=70��������CFE=�� ���ȣ�
��2����ͼ1�е���B=x����ACB=y������CFE=�� �������ú�x��y�Ĵ���ʽ��ʾ��
��3����ͼ2������ABC�Ƕ۽������Σ������������䣬��2���еĽ��ۻ���������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���D��E��F�ֱ���AB��BC��CA���е㣬AH�DZ�BC�ϵĸߣ�
��1����֤���ı���ADEF��ƽ���ı��Σ�
��2����֤����DHF=��DEF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
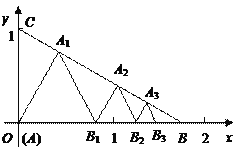
����Ŀ����ͼ��ʾ����֪����A(0��0)��B��![]() ��0����C��0��1������ABC���������ȱ������Σ�ʹһ����x���ϣ���һ��������BC���ϣ������ĵȱ������ηֱ��ǵ�1����AA1B1����2����B1A2B2����3����B2A3B3���������
��0����C��0��1������ABC���������ȱ������Σ�ʹһ����x���ϣ���һ��������BC���ϣ������ĵȱ������ηֱ��ǵ�1����AA1B1����2����B1A2B2����3����B2A3B3���������![]() ���ȱ������εı߳�����__________��
���ȱ������εı߳�����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У���ԭ��O����A��8��0����C��0��6��������OABC������OB����DΪOB���е㣬��E���߶�AB�ϵĶ��㣬����DE����DF��DE����OA�ڵ�F������EF����֪��E��A���������ÿ��1����λ���ȵ��ٶ����߶�AB���ƶ������ƶ�ʱ��Ϊt�룮

��1����ͼ1����t=3ʱ����DF�ij���
��2����ͼ2������E���߶�AB���ƶ��Ĺ����У���DEF�Ĵ�С�Ƿ����仯������仯����˵�����ɣ�������䣬�����tan��DEF��ֵ��
��3������AD����AD����DEF�ֳɵ������ֵ����֮��Ϊ1��2ʱ������Ӧ��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������в���ʽ��
��1��![]()
��2��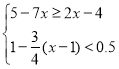
��3��2x��1��x��x��5
��4��![]()
��5��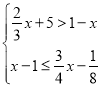
��6��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ֽƬ![]() �У�
��![]() ��
��![]() ��
��![]() ������ֽƬ�ع���
������ֽƬ�ع���![]() ��ֱ���۵���ʹ��
��ֱ���۵���ʹ��![]() ����б��
����б��![]() �ϵ�һ��
�ϵ�һ��![]() �����ۺۼ�Ϊ
�����ۺۼ�Ϊ![]() ����ͼ1������ȥ
����ͼ1������ȥ![]() ��õ�˫��
��õ�˫��![]() ����ͼ2���������ű�
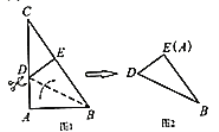
����ͼ2���������ű�![]() ij�����ֱ�߽�˫�������μ�����ʹ��չ�����ƽ��ͼ������һ����ƽ���ı��Σ�������ƽ���ı��ε��ܳ�Ϊ__________cm��
ij�����ֱ�߽�˫�������μ�����ʹ��չ�����ƽ��ͼ������һ����ƽ���ı��Σ�������ƽ���ı��ε��ܳ�Ϊ__________cm��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com