
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.

(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
【答案】(1)3;(2)∠DEF的大小不变,tan∠DEF=![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题(1)当t=3时,点E为AB的中点,由三角形的中位线定理得出DE∥EA,DE=![]() OA=4,再由矩形的性质证出DE⊥AB,得出∠OAB=∠DEA=90°,证出四边形DFAE是矩形,得出DF=AE=3即可;
OA=4,再由矩形的性质证出DE⊥AB,得出∠OAB=∠DEA=90°,证出四边形DFAE是矩形,得出DF=AE=3即可;
(2)作DM⊥OA于点M,DN⊥AB于N,证明四边形DMAN是矩形,得出∠MDN=90°,DM∥AB,DN∥OA,由平行线得出比例式![]() ,
,![]() ,由三角形中位线定理得出DM=
,由三角形中位线定理得出DM=![]() AB=3,DN=
AB=3,DN=![]() OA=4,证明ΔDMF∽ΔDNE,得出
OA=4,证明ΔDMF∽ΔDNE,得出![]() ,再由三角函数的定义即可得解;
,再由三角函数的定义即可得解;
(3)作DM⊥OA于M,DN⊥AB于N,若AD将ΔDEF的面积分为1:2的两部分,设AD交EF于点G,则点G为EF的三等分点.
①当点E到达中点之前时,NE=3-t,由ΔDMF∽ΔDNE得:MF=![]() ,求出AF=4+MF=
,求出AF=4+MF=![]() ,得出G(
,得出G(![]() ,
,![]() ),求出直线AD的解析式为y=-
),求出直线AD的解析式为y=-![]() +6,把G(
+6,把G(![]() ,
,![]() )代入即可求出t的值;
)代入即可求出t的值;
②当点超过中点之后,NE=t-3,由由ΔDMF∽ΔDNE得:MF=![]() ,求出AF=4-MF=
,求出AF=4-MF=![]() ,得出G(
,得出G(![]() ,
,![]() ),代入直线AD的解析式y=-
),代入直线AD的解析式y=-![]() +6即可求出t的值;
+6即可求出t的值;
试题解析: (1)当t=3时,点E为AB的中点,
∵A(8,0),C(0,6),
∴OA=8,OC=6,
∵点D为OB的中点,
∴DE∥OA,DE=![]() OA=4,
OA=4,
∵四边形OABC是矩形,
∴OA⊥AB,
∴DE⊥AB,
∴∠OAB=∠DEA=90°,
又∵DF⊥DE,
∴∠EDF=90°,
∴四边形DFAE是矩形,
∴DF=AE=3;
(2)∠DEF的大小不变;理由如下:
作DM⊥OA于M,DN⊥AB于N,如图2所示:
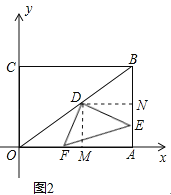
∵四边形OABC是矩形,
∴OA⊥AB,
∴四边形DMAN是矩形,
∴∠MDN=90°,DM∥AB,DN∥OA,
∴![]() ,
,![]() ,
,
∵点D为OB的中点,
∴M、N分别是OA、AB的中点,
∴DM=![]() AB=3,DN=
AB=3,DN=![]() OA=4,
OA=4,
∵∠EDF=90°,
∴∠FDM=∠EDN,
又∵∠DMF=∠DNE=90°,
∴△DMF∽△DNE,
∴![]() ,
,
∵∠EDF=90°,
∴tan∠DEF=![]() ;
;
(3)作DM⊥OA于M,DN⊥AB于N,
若AD将△DEF的面积分成1:2的两部分,
设AD交EF于点G,则点G为EF的三等分点;
①当点E到达中点之前时,如图3所示,NE=3﹣t,

由△DMF∽△DNE得:MF=![]() (3﹣t),
(3﹣t),
∴AF=4+MF=﹣![]() t+
t+![]() ,
,
∵点G为EF的三等分点,
∴G(![]() ,
,![]() ),
),
设直线AD的解析式为y=kx+b,
把A(8,0),D(4,3)代入得:![]() ,
,
解得: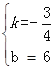 ,
,
∴直线AD的解析式为y=﹣![]() x+6,
x+6,
把G(![]() ,
,![]() )代入得:t=
)代入得:t=![]() ;
;
②当点E越过中点之后,如图4所示,NE=t﹣3,
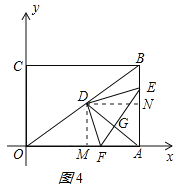
由△DMF∽△DNE得:MF=![]() (t﹣3),
(t﹣3),
∴AF=4﹣MF=﹣![]() t+
t+![]() ,
,
∵点G为EF的三等分点,
∴G(![]() ,
,![]() ),
),
代入直线AD的解析式y=﹣![]() x+6得:t=
x+6得:t=![]() ;
;
综上所述,当AD将△DEF分成的两部分的面积之比为1:2时,t的值为![]() 或
或![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )

A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
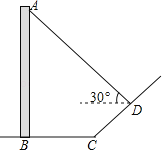
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一套西装送一条领带;②西装和领带都按定价的![]() 付款.
付款.
现某客户要到该服装厂购买西装20套,领带![]() 条(
条(![]() );
);
(1)若该客户按方案①购买,需付款____________________元(用含![]() 的代数式表示);若该客户按方案②购买,需付款__________________元(用含
的代数式表示);若该客户按方案②购买,需付款__________________元(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
(3)若![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设![]() ,
,![]() ,
,![]() ,请探索
,请探索![]() ,
,![]() ,
,![]() 满足的等量关系。
满足的等量关系。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,同底数幂的乘法法则为:am·an=am+n(其中a≠0,m,n为正整数),类似地我们规定关于任意正整数m,n的一种新运算:h(m+n)=h(m)·h(n),请根据这种新运算填空:
(1)若h(1)=![]() ,则h(2)=________;
,则h(2)=________;
(2)若h(1)=k(k≠0),则h(n)·h(2017)=________(用含n和k的代数式表示,其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于E,CF⊥BD于E,图中全等三角形有( )
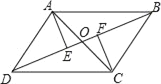
A. 3对 B. 5对 C. 6对 D. 7对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AC=10,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是 ( )
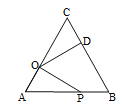
A. 5B. 6C. 7D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民李金上星期六买进某公司的股票,每股![]() 元,下表为本周内该股票的涨跌情况:
元,下表为本周内该股票的涨跌情况:
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌(与前一天相比) |
|
|
|
|
|
|
星期三收盘时,每股是________元;本周内最高价是每股________元, 最低价是每股______元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com