练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】股民李金上星期六买进某公司的股票，每股元，下表为本周内该股票的涨跌情况：

    星期

    一

    二

    三

    四

    五

    六

    每股涨跌(与前一天相比)

    星期三收盘时，每股是________元；本周内最高价是每股________元， 最低价是每股______元．

    【答案】29 30.5 27.5

    【解析】

    由上星期六买进时的股价，根据表格中的数据求出本周每天的股价即可得到结果．

    星期一的股价为：27+1.5=28.5，

    星期二的股价为：28.5-1=27.5，

    星期三的股价为：27.5+1.5=29，

    星期四的股价为：29+0.5=29.5，

    星期五的股价为：29.5+1=30.5，

    星期六的股价为：30.5-0.5=30，

    ∴星期三收盘时，每股是29元，本周内最高价是每股30.5元，最低价是每股27.5元，

    故答案为：29，30.5，27.5

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC、连结OB，点D为OB的中点，点E是线段AB上的动点，连结DE，作DF⊥DE，交OA于点F，连结EF．已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒．

    （1）如图1，当t=3时，求DF的长．

    （2）如图2，当点E在线段AB上移动的过程中，∠DEF的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠DEF的值．

    （3）连结AD，当AD将△DEF分成的两部分的面积之比为1：2时，求相应的t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把四张形状大小完全相同的小长方形卡片（如图1）按两种不同的方式，不重叠地放在一个底面为长方形（一边长为4）的盒子底部（如图2、图3），盒子底面未被卡片覆盖的部分用阴影表示．已知阴影部分均为长方形，且图2与图3阴影部分周长之比为5：6，则盒子底部长方形的面积为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是2015年12月月历．

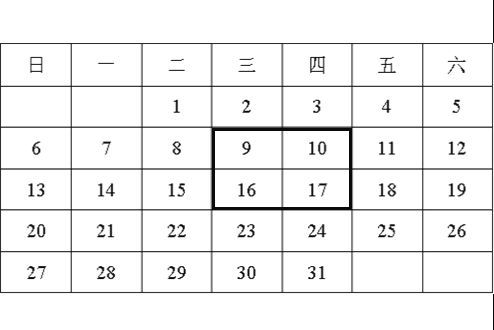
    （1）如图，用一正方形框在表中任意框往4个数，记左上角的一个数为x，则另三个数用含x的式子表示出来，从小到大依次是 ， ， ．

    （2）在表中框住四个数之和最小记为a1，和最大记为a2，则a1+a2= ．

    （3）当（1）中被框住的4个数之和等于76时，x的值为多少？

    （4）在（1）中能否框住这样的4个数，它们的和等于92？若能，则求出x的值；若不能，则说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在Rt△ABC中，∠C=90°，BC=6cm,AC=8 cm，AB=10 cm. 现有一动点P，从A点出发，沿着三角形的边AC-CB-BA运动，回到A点停止，速度为1 cm/s，设运动时间为t s.

    （1）当t=_______时，△ABC的周长被线段AP平分为相等的两部分.

    （2）当t=_______时，△APC的面积等于△ABC面积的一半.

    （3）还有一个△DEF，∠E=90°，如图②所示，DE=4cm，DF=5cm，∠D=∠A. 在△ABC的边上，若另外有一个动点Q，与P 同时从A点出发，沿着边AB-BC-CA运动，回到点A停止. 在两点运动过程中某一时刻，恰好△APQ与△DEF全等，则点Q的运动速度 cm/s.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点若点D为BC边的中点，点M为线段EF上一动点，则周长的最小值为　　

    A. 6 B. 8 C. 10 D. 12

    查看答案和解析>>

    科目：初中数学 来源： 题型：

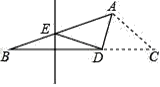
    【题目】如图，在△ABC 中，∠BAC=120°，点 D 是 BC 上一点，BD 的垂直平分线交 AB 于点E，将△ACD 沿 AD 折叠，点 C 恰好与点 E 重合，则∠B 等于_______°；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

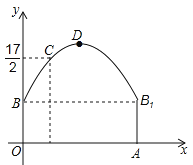
    【题目】（12分）如图所示是隧道的截面由抛物线和长方形构成，长方形的长是12 m，宽是4 m．按照图中所示的直角坐标系，抛物线可以用y=x2+bx+c表示，且抛物线上的点C到OB的水平距离为3 m，到地面OA的距离为m.

    （1）求抛物线的函数关系式，并计算出拱顶D到地面OA的距离；

    （2）一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向车道，那么这辆货车能否安全通过？

    （3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面的推理过程，在括号内填上推理的依据，如图：

    ∵∠1+∠2=180°，∠2+∠4=180°(已知)

    ∴∠1=∠4( )

    ∴c∥a( )

    又∵∠2+∠3=180°(已知 )

    ∠3=∠6( )

    ∴∠2+∠6=180°( )

    ∴a∥b( )

    ∴c∥b( )

    查看答案和解析>>

    同步练习册答案