
�����龳����ͼ1��ֱ�����ǰ�ABC�У���C��90�㣬AC��BC����һ�����㹻���ĵ�ϸ��˿������ֱ�ǵĶ���D����ֱ�����ǰ�ABC��б��AB�ϣ��ٽ���ֱ���Ƶ�D��ת����ʹ�����߷ֱ������ǰ��AC�ߡ�BC�߽���P��Q���㡣
����̽������1������ת�����У�
����ͼ2����AD��BDʱ���߶�DP��DQ�к�������ϵ����˵�����ɡ�
����ͼ3����AD��2BDʱ���߶�DP��DQ�к�������ϵ����˵�����ɡ�
�۸�����Ԣ١��ڵ�̽���������д����AD��nBDʱ��DP��DQ�����������ϵΪ_______________��ֱ��д�����ۣ�����֤����
��2����AD��BDʱ����AB��20������PQ�����DPQ�����ΪS������ת�����У�S�Ƿ������Сֵ�����ֵ�������ڣ������Сֵ�����ֵ���������ڣ���˵�����ɡ�

ͼ1 ͼ2 ͼ3
��1����DP��DQ
���ɣ�����CD��
 ����ABC�ǵ���ֱ�������Σ�
����ABC�ǵ���ֱ�������Σ�
 ����A����DCQ����ADC��90�㣬���ADP����PDC����CDQ����PDC��90�㣬
����A����DCQ����ADC��90�㣬���ADP����PDC����CDQ����PDC��90�㣬
���ADP����CDQ�����ADP�ա�CDQ��
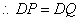
��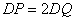 ��
��
���ɣ���ͼ������D��DM��AC��DN��BC������ֱ�ΪM��N��

���DMP����DNQ��90�㣬���MDP����NDQ��
���DPM�ס�DQN�� ��
��
�ߡ�AMD����DNB��90�㣬��A����B��
���AMD�ס�BND��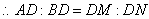 ��
��
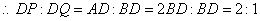 ��
��
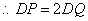 ��
��
��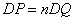 ��
��
��2�����ڣ��� ���ɣ�1����֪
���ɣ�1����֪ ��
��

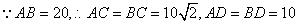 ��
��
��DP��ACʱ��x��С����Сֵ��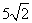 ����ʱ��S����Сֵ��
����ʱ��S����Сֵ��
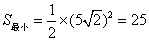
����P���A�غ�ʱ��x������ֵ��10����ʱ��S�����ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
һ���������£�3��6��7��2��3��4��3��6����ô�������ݵ���λ���������ֱ���
A��3��3 B��3.5��3 C��4��3 D��3.5��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����������ֱ��������2��1����3����4�IJ�����Ƭ�����dz�����������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ�����ſ�Ƭ���������ȡһ�Ų��Żأ����ÿ�Ƭ�ϵ����ּ�Ϊm�����������ȡһ�ţ�����Ƭ�ϵ����ּ�Ϊn��
��1���뻭����״ͼ��д����m��n�����п��ܵĽ����
��2������ѡ����m��n��ʹһ�κ���y=mx+n��ͼ���ڶ������������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
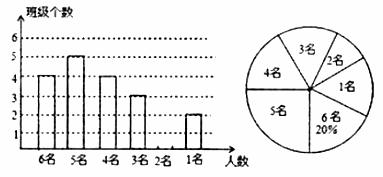
Ϊ��Ӧ������2014�괴�����Ҽ��������еĺ��٣�ijУ���꼶����������ΪȰ��־Ը������������ͳ�ƣ�����ͳ��������6����5����4����3����2����1�������������������������������������ͳ��ͼ��
��1������꼶ƽ��ÿ���ж���������ΪȰ��־Ը�ߣ���������ͼ����������
��2����У�������ܿ�չ����ʵ������Ӱ��꼶ֻ��2��������ΪȰ��־Ը�ߵİ༶����ѡ�����������б�����״ͼ�ķ����������ѡ������ΪȰ��־Ը������������ͬһ�༶�ĸ��ʡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
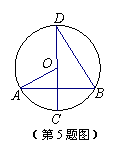
��ͼ����O��ֱ��CD��AB����AOC=50�㣬���CDB��СΪ
A��25�� B��30�� C��40�� D��50��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
PM 2.5��ָ������ֱ��С�ڻ����0.0000025 m�Ŀ������0.0000025�ÿ�ѧ��������ʾΪ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ������OABC�У�A��6��0����C��0��2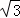 ����D��0��3
����D��0��3 ��������l����D����x��ƽ�У���P��Q�ֱ���l��x���������϶��㣬�����PQO=60�㣮
��������l����D����x��ƽ�У���P��Q�ֱ���l��x���������϶��㣬�����PQO=60�㣮
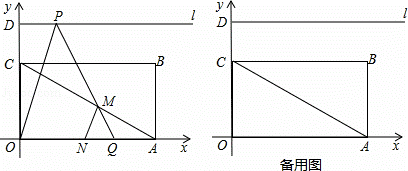
��1���ٵ�B�������������ڡ�CAO=�� �ȣ��۵���Q���A�غ�ʱ����P������Ϊ �� ����ֱ��д���𰸣�
��2����OA���е�ΪN��PQ���߶�AC�ཻ�ڵ�M���Ƿ���ڵ�P��ʹ��AMNΪ���������Σ������ڣ���ֱ��д����P�ĺ�����Ϊm���������ڣ���˵�����ɣ�
��3�����P�ĺ�����Ϊx����OPQ�����OABC���ص����ֵ����ΪS������ S��x�ĺ�����ϵʽ����Ӧ���Ա�
S��x�ĺ�����ϵʽ����Ӧ���Ա� ��x��ȡֵ��Χ��
��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
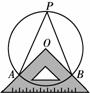
��ͼ�������ǰ��ֱ�Ƕ�����ڡ�O��Բ���ϣ�����ֱ�DZ߷ֱ�O��A��B���㣬��P���Ż�AB�ϣ������A��B���غϣ�����PA��PB.���APB�Ĵ�СΪ �ȣ�
 |
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com