
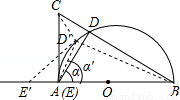
(本题满分8分)如图所示,AC⊥AB, ,AC=2,点D是以AB为直径的半圆O 上一动点,DE⊥CD交直线AB于点E,设
,AC=2,点D是以AB为直径的半圆O 上一动点,DE⊥CD交直线AB于点E,设 .
.

(1)当 时,求弧BD的长;
时,求弧BD的长;
(2)当 时,求线段BE的长;
时,求线段BE的长;
(3)若要使点E在线段BA的延长线上,则 的取值范围是________ _.(直接写出答案)
的取值范围是________ _.(直接写出答案)
(1)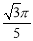 ;(2)
;(2)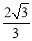 ;(3)
;(3)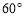 <
<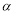 <
<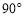 .
.
【解析】
试题分析:(1)首先连接OD,由圆周角定理,可求得∠DOB的度数,又由⊙O的直径为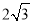 ,即可求得其半径,然后由弧长公式,即可求得答案;
,即可求得其半径,然后由弧长公式,即可求得答案;
(2)首先证得△ACD∽△BED,然后由相似三角形的对应边成比例,可得 ,继而求得答案;
,继而求得答案;
(3)首先求得A与E重合时α的度数,则可求得点E在线段BA的延长线上时,α的取值范围.
试题解析:(1)连接OD,在⊙O中,∵∠DAB=18°,∴∠DOB=2∠DAB=36°.
又∵AB=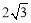 ,∴
,∴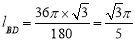 ;
;
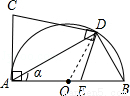
(2)∵AB为⊙O的直径,∴∠ADB=90°,又∵∠DAB=90°,AB=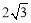 ,
,
∴BD=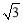 ,AD=3.
,AD=3.
又∵AC⊥AB, ∴∠CAB=90°, ∴∠CAD+∠DAB=90°,
又∵∠ADB=90°, ∴∠DAB+∠B=90°,∴∠CAD=∠B,
又∵DE⊥CD,∴∠CDE=90°,∴∠CDA+∠ADE=90°,
又∵∠ADE+∠EDB=90°,∴∠CDA=∠EDB,∴△CDA∽△EDB,
∴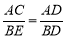 ,又∵AC=2, ∴
,又∵AC=2, ∴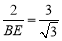 ,∴
,∴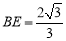 ;
;
(3)如图,当E与A重合时,
∵AB是直径,AD⊥CD,∴∠ADB=∠ADC=90°,∴C,D,B共线,
∵AC⊥AB,∴在Rt△ABC中,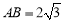 ,AC=2,∴tan∠ABC=
,AC=2,∴tan∠ABC=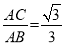 ,∴∠ABC=30°,
,∴∠ABC=30°,
∴α=∠DAB=90°﹣∠ABC=60°,
当E′在BA的延长线上时,如图,可得∠D′AB>∠DAB>60°,
∵0°<α<90°,∴α的取值范围是:60°<α<90°.
故答案为:60°<α<90°.
考点:1.相似三角形的判定与性质;2.圆周角定理;3.弧长的计算.


科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,AB是⊙O的直径,点D在AB的延长线上,过点D作DC切⊙O于点C,若∠A=35°,则∠D=____ ____°

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市八年级上学期期中考试数学试卷(解析版) 题型:选择题
在等腰三角形ABC中,∠ABC=120°,点P是底边BC上一个动点,点M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )

A.2 B. C.4 D.
C.4 D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市滨湖区九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分7分) 已知关于 的方程
的方程 .
.
(1)试说明:无论 取什么实数值,方程总有实数根;
取什么实数值,方程总有实数根;
(2)若等腰△ABC的一边长a为1,另两边长 、c恰好是这个方程的两个实数根,求△ABC的周长.
、c恰好是这个方程的两个实数根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期高效课堂调研数学试卷(解析版) 题型:解答题
(本题满分9分)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
(1)在△ABC内放入正方形纸片DEFG,使边EF在斜边AB上,点D、G分别在AC、BC上。则正方形的边长为 ;
(2)类似第(1)小题,使正方形纸片一条边都在AB上,若在△ABC内并排(不重叠)放入两个小正方形,且只能放入两个,试确定小正方形边长的范围;

(3)在△ABC内并排放入(不重叠)边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放 个小正方形纸片.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,在平面直角坐标系中,点C的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O出发沿 轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD=
轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.当S△BCD= 时,t的值为 ( )
时,t的值为 ( )

A.2或2+3 B.2或2+3
B.2或2+3 C.3或3+5
C.3或3+5 D.3或3+5
D.3或3+5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com