Question

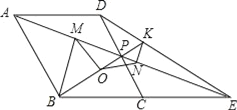
【题目】如图，菱形ABCD中，点P是CD的中点，∠BCD=60°，射线AP交BC的延长线于点E，射线BP交DE于点K，点O是线段BK的中点，作BM⊥AE于点M，作KN⊥AE于点N，连结MO、NO，以下四个结论：①△OMN是等腰三角形；②tan∠OMN=；③BP=4PK；④PMPA=3PD2，其中正确的是（　　）

A. ①②③ B. ①②④ C. ①③④ D. ②③④

Answer 1

【答案】B

【解析】试题分析：根据菱形的性质得到AD∥BC，根据平行线的性质得到对应角相等，根据全等三角形的判定定理△ADP≌△ECP，由相似三角形的性质得到AD=CE，作PI∥CE交DE于I，根据点P是CD的中点证明CE=2PI，BE=4PI，根据相似三角形的性质得到=，得到BP=3PK，故③错误；作OG⊥AE于G，根据平行线等分线段定理得到MG=NG，又OG⊥MN，证明△MON是等腰三角形，故①正确；根据直角三角形的性质和锐角三角函数求出∠OMN=，故②正确；然后根据射影定理和三角函数即可得到PMPA=3PD2，故④正确．

解：作PI∥CE交DE于I，

∵四边形ABCD为菱形，

∴AD∥BC，

∴∠DAP=∠CEP，∠ADP=∠ECP，

在△ADP和△ECP中，

，

∴△ADP≌△ECP，

∴AD=CE，

则，又点P是CD的中点，

∴=，

∵AD=CE，

∴=，

∴BP=3PK，

故③错误；

作OG⊥AE于G，

∵BM丄AE于M，KN丄AE于N，

∴BM∥OG∥KN，

∵点O是线段BK的中点，

∴MG=NG，又OG⊥MN，

∴OM=ON，

即△MON是等腰三角形，故①正确；

由题意得，△BPC，△AMB，△ABP为直角三角形，

设BC=2，则CP=1，由勾股定理得，BP=，

则AP=，

根据三角形面积公式，BM=，

∵点O是线段BK的中点，

∴PB=3PO，

∴OG=BM=，

MG=MP=，

tan∠OMN==，故②正确；

∵∠AP=90°，BM⊥AP，

∴PB2=PMPA，

∵∠BCD=60°，

∴∠ABC=120°，

∴∠PBC=30°，

∴∠BPC=90°，

∴PB=PC，

∵PD=PC，

∴PB2=3PD，

∴PMPA=3PD2，故④正确．

故选B．