
 在直角坐标系中,点A的坐标是(3,0),点P在第一象限内的直线y=-x+4上.设点P的坐标为(x,y).
在直角坐标系中,点A的坐标是(3,0),点P在第一象限内的直线y=-x+4上.设点P的坐标为(x,y).分析 (1)根据点A坐标可得出OA的长度,再由点P在第一象限内的直线y=-x+4上,即可得出y与x之间的关系以及x的取值范围,代入三角形的面积公式即可得出结论;
(2)将S=$\frac{1}{2}$代入(1)得出的关系式中求出x值,再由点P在直线y=-x+4上即可求出y值,从而得出点P的坐标;
(3)分OA、OP、PA为对角线三种情况考虑,根据平行四边形的性质即可得出点Q的坐标.
解答 解:(1)∵点A的坐标是(3,0),
∴OA=3,
∴S=$\frac{1}{2}$OA•yP=$\frac{3}{2}$y.
∵点P(x,y)在第一象限内的直线y=-x+4上,
∴y=-x+4(0<x<4),
∴S=$\frac{3}{2}$(-x+4)=-$\frac{3}{2}$x+6(0<x<4).
(2)令S=-$\frac{3}{2}$x+6中S=$\frac{1}{2}$,则-$\frac{3}{2}$x+6=$\frac{1}{2}$,
解得:x=$\frac{11}{3}$,y=-x+4=$\frac{1}{3}$,
∴当S=$\frac{1}{2}$时,点P的坐标为($\frac{11}{3}$,$\frac{1}{3}$).
(3)以P、O、A、Q为顶点的平行四边形分三种情况(如图所示):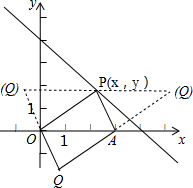
①当OA为对角线时,
∵P($\frac{11}{3}$,$\frac{1}{3}$),O(0,0),A(3,0),
∴Q(0+3-$\frac{11}{3}$,0+0-$\frac{1}{3}$),即(-$\frac{2}{3}$,-$\frac{1}{3}$);
②当OP为对角线时,
∵P($\frac{11}{3}$,$\frac{1}{3}$),O(0,0),A(3,0),
∴Q(0+$\frac{11}{3}$-3,0+$\frac{1}{3}$-0),即(-$\frac{2}{3}$,$\frac{1}{3}$);
③当PA为对角线时,
∵P($\frac{11}{3}$,$\frac{1}{3}$),O(0,0),A(3,0),
∴Q(3+$\frac{11}{3}$-0,0+$\frac{1}{3}$-0),即($\frac{20}{3}$,$\frac{1}{3}$).
综上可知:在(2)的条件下,若以P、O、A、Q为顶点构成平行四边形,第四个顶点Q的坐标为(-$\frac{2}{3}$,-$\frac{1}{3}$)、(-$\frac{2}{3}$,$\frac{1}{3}$)、($\frac{20}{3}$,$\frac{1}{3}$).
点评 本题考查了一次函数图象上点的坐标特征、三角形的面积以及平行四边形的性质,解题的关键是:(1)根据三角形的面积公式找出S关于x的函数关系式;(2)令S=$\frac{1}{2}$求出x值;(3)分三种情况考虑.本题属于中档题,难度不大,解决该题型题目时,根据平行四边形的性质以及三个顶点坐标求出第四个顶点的坐标是关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:选择题
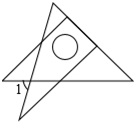 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )| A. | 60° | B. | 75° | C. | 65° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | BC=AB+AC | B. | AC2=AB2+BC2 | C. | AB2=AC2+BC2 | D. | BC2=AB2+AC2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 按如图所示的程序计算,若开始输入x的值为6,我们发现第一次得到的结果为3,第2次得到的结果为10,第3次得到的结果为5…请你探索第4次得到的结果为12,第2011次得到的结果为3.
按如图所示的程序计算,若开始输入x的值为6,我们发现第一次得到的结果为3,第2次得到的结果为10,第3次得到的结果为5…请你探索第4次得到的结果为12,第2011次得到的结果为3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}{a^4}{b^2}$ | B. | $\frac{1}{8}{a^6}{b^3}$ | C. | $-\frac{1}{8}{a^6}{b^3}$ | D. | $-\frac{1}{8}{a^5}{b^3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | $\sqrt{10}$ | C. | $\root{4}{10}$ | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com