Question

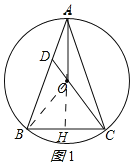
【题目】如图，△ABC内接于⊙O，AB＝AC，CO的延长线交AB于点D.

(1)求证：AO平分∠BAC；

(2)若BC＝6，sin∠BAC＝，求AC和CD的长．

Answer 1

【答案】(1)证明见解析；（2）AC＝ ， CD＝ ,

【解析】分析：（1）延长AO交BC于H，连接BO，证明A、O在线段BC的垂直平分线上，得出AO⊥BC，再由等腰三角形的性质即可得出结论；（2）延长CD交⊙O于E，连接BE，则CE是⊙O的直径，由圆周角定理得出∠EBC=90°，∠E=∠BAC，得出sinE=sin∠BAC，求出CE=BC=10，由勾股定理求出BE=8，证出BE∥OA，得出，求出OD=，得出CD=，而BE∥OA，由三角形中位线定理得出OH=BE=4，CH=BC=3，在Rt△ACH中，由勾股定理求出AC的长即可．

本题解析：

解：(1)证明：延长AO交BC于H，连接BO.

∵AB＝AC，OB＝OC，

∴A，O在线段BC的垂直平分线上．∴AO⊥BC.

又∵AB＝AC，∴AO平分∠BAC.

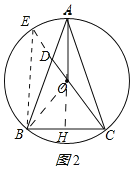
(2)延长CD交⊙O于E，连接BE，则CE是⊙O的直径．

∴∠EBC＝90°，BC⊥BE.

∵∠E＝∠BAC，∴sinE＝sin∠BAC.

∴＝.∴CE＝BC＝10.

∴BE＝＝8，OA＝OE＝CE＝5.

∵AH⊥BC，∴BE∥OA.

∴＝，即＝，

解得OD＝.∴CD＝5＋＝.

∵BE∥OA，即BE∥OH，OC＝OE，∴OH是△CEB的中位线．

∴OH＝BE＝4，CH＝BC＝3.∴AH＝5＋4＝9.

在Rt△ACH中，AC＝＝＝3.