
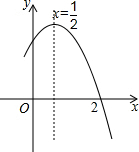 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0).下列结论:①ac<0,②4a+2b+c<0,③a-b+c=0,④若(-2,y1)(-3,y2)是抛物线上的两点,则y1<y2.其中正确结论的个数是( )
如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0).下列结论:①ac<0,②4a+2b+c<0,③a-b+c=0,④若(-2,y1)(-3,y2)是抛物线上的两点,则y1<y2.其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据抛物线开口向下,可得a<0,抛物线与y轴的正半轴相交可得c>0,可对①进行判断;由于x=2时,对应的函数值为0,由此可对②进行判断;由抛物线对称轴为x=$\frac{1}{2}$,根据抛物线的对称性可得到抛物线与x轴另一个交点坐标为(-1,0),则a-b+c=0,可对③进行判断;点(-2,y1)和(-3,y2)在对称轴左侧,y随x的增大而增大,可对④进行判断.
解答 解:①∵二次函数的图象开口向下,
∴a<0,
∵二次函数的图象交y轴的正半轴于一点,
∴c>0,
∴ac<0.
故①正确;
②把x=2代入y=ax2+bx+c得:y=4a+2b+c,
∵抛物线经过点(2,0),
∴当x=2时,y=0,即4a+2b+c=0
故②错误;
③∵对称轴是直线x=$\frac{1}{2}$,且经过点(2,0),
∴抛物线与x轴另一个交点坐标为(-1,0),
∴a-b+c=0,所以③正确;
④∵点(-2,y1)和(-3,y2)在对称轴左侧,
∴y随x的增大而增大,
∵-2>-3,
∴y1>y2,
故④错误;
综上所述,正确的结论是①③.
故选B.
点评 本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a<0,抛物线开口向下;对称轴为直线x=-$\frac{b}{2a}$;抛物线与y轴的交点坐标为(0,c).


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:解答题
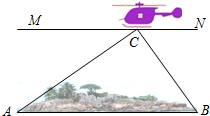 如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A、B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A、B的距离.
如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A、B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A、B的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
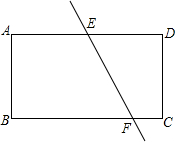 教材“8.3实际问题与二元一次方程组”探究2:“据统计资料,甲乙两种农作物的单位面积产量的比是1:2,现要把一块长200m,宽为100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲,乙两种作物的总产量的比是3:4“小明在探究完后提出这样一个想法:如果把原题中“分为两块小长方形土地”“分割成两块梯形土地,如图所示”,其他条件不变,这样划分这块土地,还能使甲,乙两种作物的总产量的比是3:4吗?
教材“8.3实际问题与二元一次方程组”探究2:“据统计资料,甲乙两种农作物的单位面积产量的比是1:2,现要把一块长200m,宽为100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲,乙两种作物的总产量的比是3:4“小明在探究完后提出这样一个想法:如果把原题中“分为两块小长方形土地”“分割成两块梯形土地,如图所示”,其他条件不变,这样划分这块土地,还能使甲,乙两种作物的总产量的比是3:4吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com