
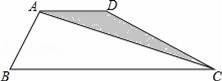
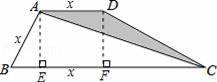
如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是 .

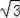
 .
.
【考点】含30度角的直角三角形;勾股定理.
【分析】如图,过点A作AE⊥BC于E,过点D作DF⊥BC于F.构建矩形AEFD和直角三角形,通过含30度角的直角三角形的性质求得AE的长度,然后由三角形的面积公式进行解答即可.
【解答】解:如图,过点A作AE⊥BC于E,过点D作DF⊥BC于F.设AB=AD=x.
又∵AD∥BC,
∴四边形AEFD是矩形形,
∴AD=EF=x.
在Rt△ABE中,∠ABC=60°,则∠BAE=30°,
∴BE=
 AB=
AB=
 x,
x,
∴DF=AE=
 =
=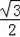
 x,
x,
在Rt△CDF中,∠FCD=30°,则CF=DF•cot30°=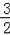
 x.
x.
又∵BC=6,
∴BE+EF+CF=6,即
 x+x+
x+x+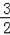
 x=6,
x=6,
解得 x=2
∴△ACD的面积是:
 AD•DF=
AD•DF=
 x×
x×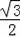
 x=
x=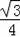
 ×22=
×22=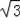
 ,
,
故答案为: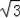
 .
.

【点评】本题考查了勾股定理,三角形的面积以及含30度角的直角三角形.解题的难点是作出辅助线,构建矩形和直角三角形,目的是求得△ADC的底边AD以及该边上的高线DF的长度.


科目:初中数学 来源: 题型:
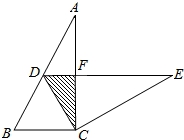
如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )
A.30,2 B.60,2 C.60,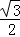 D.60,
D.60,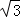
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律,如:第三行的三个数(1、2、1)恰好对应着(a+b)2的展开式a2+2ab+b2的系数;第四行的四个数恰好对应着(a+b)3=a3+3a2b+3ab2+b3的系数,根据数表中前五行的数字所反映的规律,回答:
(1)图中第六行括号里的数字分别是__________;(请按从左到右的顺序填写)
(2)(a+b)4=__________;
(3)利用上面的规律计算求值:(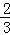 )4﹣4×(
)4﹣4×(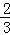 )3+6×(
)3+6×(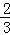 )2﹣4×
)2﹣4×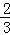 +1.
+1.
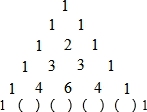
查看答案和解析>>
科目:初中数学 来源: 题型:
为落实国家“三农”政策,某地政府组织40辆汽车装运A、B、C三种农产品共200吨到外地销售,按计划,40辆车都要装运,每辆车只能装运同一种农产品,且必须装满,根据下表提供的信息,解答下列问题:
| 农产品种类 | A | B | C |
| 每辆汽车的装载量(吨) | 4 | 5 | 6 |
(1)如果装运C种农产品需13辆汽车,那么装运A、B两种农产品各需多少辆汽车?
(2)如果装运每种农产品至少需要11辆汽车,那么车辆的装运方案有几种?写出每种装运方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
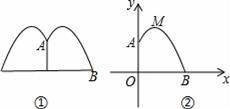
如图是某公园一圆形喷水池,水流在各个方向沿形状相同的抛物线落下,建立如图所示的坐标系,如果喷头所在处A(0,1.25),水流路线最高处M(1,2.25),如果不考虑其他因素,那么水池的半径至少要 m,才能使喷出的水流不至落到池外.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com