
【题目】如图,反比例函数![]() (
(![]() ,)的图象与直线
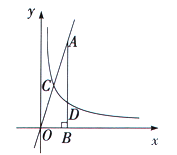
,)的图象与直线![]() 相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确定一点M,使点M到C、D两点距离之和d=MC+MD最小,求点M的坐标.
【答案】(1)1;(2)(![]() ,
, ![]() );(3) M(0,2
);(3) M(0,2![]() ﹣2).
﹣2).
【解析】(1)根据A坐标,以及AB=3BD求出D坐标,代入反比例解析式求出k的值;
(2)直线y=3x与反比例解析式联立方程组即可求出点C坐标;
(3)作C关于y轴的对称点C′,连接C′D交y轴于P,则P点即为所求,利用待定系数法求出直线C′D的解析式,进而可得出M点坐标.
解:A(1,3),
∴AB=3,OB=1,
∵AB=3BD,
∴BD=1,
∴D(1,1)
将D坐标代入反比例解析式得:k=1;
(2)由(1)知,k=1,
∴反比例函数的解析式为;y=![]() ,解:
,解:![]() ,
,
解得: 或
或 ,
,
∵x>0,
∴C(![]() ,
,![]() );
);
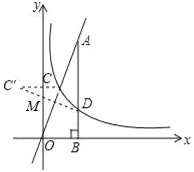
(3)如图,作C关于y轴的对称点C′,连接C′D交y轴于M,则d=MC+MD最小,
∴C′(﹣![]() ,
,![]() ),
), 
设直线C′D的解析式为:y=kx+b,
∴ ,∴
,∴![]() ,
,
∴y=(﹣3+2![]() )x+2
)x+2![]() ﹣2,
﹣2,
当x=0时,y=2![]() ﹣2, ∴M(0,2
﹣2, ∴M(0,2![]() ﹣2).
﹣2).
“点睛”此题考查的是反比例函数综合题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,以及直线与反比例的交点求法,熟练掌握待定系数法是解本题的关键.


科目:初中数学 来源: 题型:
【题目】 (2016湖南常德第21题)某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com