
����Ŀ��������10�֣�ij�̳�����A��B����Ʒ�ƵĽ�ѧ�豸�������ֽ�ѧ�豸�Ľ��ۺ��ۼ����±���ʾ��
A | B | |
���ۣ���Ԫ/�ף� | 1.5 | 1.2 |
�ۼۣ���Ԫ/�ף� | 1.65 | 1.4 |
���̳��ƻ��������ֽ�ѧ�豸�����ף�����66��Ԫ��ȫ�����ۺ�ɻ�ë����9��Ԫ��
��ë����=���ۼ� - ���ۣ�����������
��1�����̳��ƻ�����A��B����Ʒ�ƵĽ�ѧ�豸�������ף�
��2��ͨ���г����У����̳�������ԭ�ƻ��Ļ����ϣ�����A���豸�Ĺ�������������B���豸�Ĺ�����������֪B���豸���ӵ�������A���豸����������1.5���������ڹ��������ֽ�ѧ�豸�����ʽ���69��Ԫ����A���豸��������������ٶ����ף�
���𰸡���1�����̳��ƻ�����AƷ�ƵĽ�ѧ�豸20�ף�BƷ�ƵĽ�ѧ�豸30�ף���2��A���豸���������������10�ף�
��������
�����������1����AƷ�ƵĽ�ѧ�豸x�ף�BƷ�ƵĽ�ѧ�豸y�ף���������ɵ÷�����![]() ���ⷽ���鼴������̳��ƻ�����A��B����Ʒ�ƵĽ�ѧ�豸����������A���豸������������a�ף���B���豸������������1.5a�ף�������ò���ʽ1.5��20-a��+1.2��30+1.5a����69�����a��10�����ɵ�A���豸���������������10�ף�
���ⷽ���鼴������̳��ƻ�����A��B����Ʒ�ƵĽ�ѧ�豸����������A���豸������������a�ף���B���豸������������1.5a�ף�������ò���ʽ1.5��20-a��+1.2��30+1.5a����69�����a��10�����ɵ�A���豸���������������10�ף�
�����������1����AƷ�ƵĽ�ѧ�豸x�ף�BƷ�ƵĽ�ѧ�豸y�ף������⣬��
![]() ��
��
��ã�![]() ��
��
�𣺸��̳��ƻ�����AƷ�ƵĽ�ѧ�豸20�ף�BƷ�ƵĽ�ѧ�豸30�ף�
��2����A���豸������������a�ף���B���豸������������1.5a�ף������⣬��
1.5��20-a��+1.2��30+1.5a����69��
��ã�a��10��
��A���豸���������������10�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�![]() ����cΪ��ߣ���
����cΪ��ߣ���![]() ʱ����ABC��ֱ�������Σ���
ʱ����ABC��ֱ�������Σ���![]() ʱ�����ô���ʽ
ʱ�����ô���ʽ![]() ��
��![]() �Ĵ�С��ϵ�������жϡ�ABC����״�����Ƿ��ࣩ��
�Ĵ�С��ϵ�������жϡ�ABC����״�����Ƿ��ࣩ��
��1������ͨ����ͼ̽�����жϣ�����ABC���߳��ֱ�Ϊ6��8��9ʱ����ABCΪ____�����Σ�����ABC���߳��ֱ�Ϊ6��8��11ʱ����ABCΪ______�����Σ�
��2��С��ͬѧ��������̽����������IJ��룺����![]() ʱ����ABCΪ��������Σ���
ʱ����ABCΪ��������Σ���![]() ʱ����ABCΪ�۽������Σ����������С���IJ��������������⣺
ʱ����ABCΪ�۽������Σ����������С���IJ��������������⣺
��![]() ��
��![]() ʱ�����c��ʲô��Χ��ȡֵʱ����ABC��ֱ�������Ρ���������Ρ��۽������Σ�
ʱ�����c��ʲô��Χ��ȡֵʱ����ABC��ֱ�������Ρ���������Ρ��۽������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��2(x��3)2+k����ƽ��1����λ���Ⱥ���(2��3)����k��ֵ��( )
A. 2B. 1C. 0D. ��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϵ�A��ʾ������3�������A���4����λ���ȵĵ��ʾ������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��һ����ÿ������������������¼�¼���±���
���� | һ | �� | �� | �� | �� | �� | �� |
������� | 10�� | 12�� | 11�� | 9�� | 7�� | 5�� | 7�� |
������� | 2�� | 1�� | 0�� | ��1�� | ��4�� | ��5�� | ��5�� |
���²�����һ��������_____����һ���²�Ϊ_____�森
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У�O Ϊ����ԭ�㣬��� P��1��m���ں���![]() ��ͼ���ϣ��� OP Ϊ����������OPQR��������������
��ͼ���ϣ��� OP Ϊ����������OPQR�������������� ![]() ������ Q���� k=______________��
������ Q���� k=______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
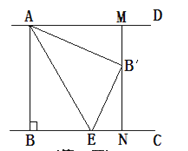
����Ŀ����ͼ����֪AD��BC��AB��BC��AB=3. ��EΪ����BC��һ�����㣬����AE������ABE��AE�۵�����B���ڵ�B����������B����AD�Ĵ��ߣ��ֱ�AD��BC�ڵ�M��N. ����B��Ϊ�߶�MN�����ȷֵ�ʱ��BE�ij�Ϊ__________________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com