练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．考虑下面两种移动电话计费方式：
    方式一方式二
    月租费/（元/月）300
    本地通话费/（元/min）0.300.40
    用函数方法解答何时两种计费方式费用相等．

    分析 根据“方式一费用=月租费+本地通话费用×通话时间；方式二费用=本地通话费用×通话时间．”即可得出y1、y2关于x的函数关系式，再根据y1=y2以找出关于x的一元一次方程，通过解方程求出x的值，由此即可得出结论．

    解答 解：由已知得：y1=0.3x+30，y2=0.4x，
    令y1=y2，即0.3x+30=0.4x，
    解得：x=300．
    故当x=300分钟时，两种计费方式费用一样多．

    点评 本题考查了一次函数的应用、解一元一次方程，解题的关键是根据数量关系找出函数关系式．本题属于基础题，难度不大，解决该题型题目时，根据数量关系找出函数关系式是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    8．二元一次方程组$\left\{\begin{array}{l}{x+y=7}\\{3x-y=5}\end{array}\right.$的解是（　　）
    A．$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$B．$\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$C．$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$D．$\left\{\begin{array}{l}{x=-2}\\{y=9}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

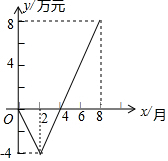    7．某超市今年年初因管理不善，效益较差，连续几个月出现亏损，后改革管理方法，实行股份制，员工积极性大增，业绩逐步上升，1-8月的累计利润y（万元）与时间x（月）之间的关系如图，根据图象回答：
    （1）求y与x之间的函数关系式；
    （2）该超市从几月份开始扭亏？
    （3）8月份获得的利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．某商场打算在年前用30000元购进一批彩灯进行销售，由于进货厂家促销，实际可以以8折的价格购进这批彩灯，结果可以比计划多购进了100盏彩灯．
    （1）该商场购进这种彩灯的实际进价为多少元？
    （2）该商场打算在实际进价的基础上，每盏灯加价50%的销售，但可能会面临滞销，因此将有20%的彩灯需要降价，以5折出售，该商场要想获利不低于15000元，应至少在购进这种彩灯多少盏？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图（1）是一个晾衣架的实物图，支架的基本图形是菱形，MN是晾衣架的一个滑槽，点P在滑槽MN上、下移动时，晾衣架可以伸缩，其示意图如图（2）所示，已知每个菱形的边长均为20cm，且AB=CD=CP=DM=20cm．

    （1）当点P向下滑至点N处时，测得∠DCE=60°时
    ①求滑槽MN的长度；
    ②此时点A到直线DP的距离是多少？
    （2）当点P向上滑至点M处时，点A在相对于（1）的情况下向左移动的距离是多少？
    （结果精确到0.01cm，参考数据 $\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

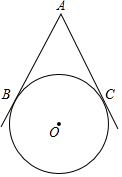    1．如图，AB、AC是◎o的两条切线，切点为B、C且∠BAC=50°，D是圆上一动点（不与B、C重合），则∠BDC的度数为（　　）
    A．130°B．65°C．50°或130°D．65°或115°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：（3.14-π）0+2cos45°-|1-$\sqrt{2}$|+（$\frac{1}{2}$）-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．今年4月，我市某中学举行了“爱我中国•朗诵比赛”活动，根据学生的成绩划分为A、B、C、D四个等级，并绘制了如下两种不完整的统计图．根据图中提供的信息，回答下列问题：
    （1）参加朗诵比赛的学生共有40人，并把条形统计图补充完整；
    （2）扇形统计图中，m=10，n=40；C等级对应扇形的圆心角为144度；
    （3）学校准备从获A等级的学生中随机选取2人，参加市举办的朗诵比赛，请利用列表法或树形图法，求获A等级的小明参加市朗诵比赛的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．阅读材料：如图1，在平面直角坐标系中，A、B两点的坐标分别为A（x1，y1），B（x2，y2），AB中点P的坐标为（xp，yp）．由xp-x1=x2-xp，得xp=$\frac{{x}_{1}+{x}_{2}}{2}$，同理yp=$\frac{{y}_{1}+{y}_{2}}{2}$，所以AB的中点坐标为（$\frac{{x}_{1}+{x}_{2}}{2}$，$\frac{{y}_{1}+{y}_{2}}{2}$）．由勾股定理得AB2=|x2-x1|2+|y2-y1|2，所以A、B两点间的距离公式为AB=$\sqrt{（{x}_{2}-{x}_{1}）^{2}+（{y}_{2}-{y}_{1}）^{2}}$．这两公式对A、B在平面直角坐标系中其它位置也成立．解答下列问题：
    （1）已知M（1，-2），N（-1，2），直接利用公式填空：MN中点坐标为（0，0），MN=2$\sqrt{5}$．
    如图2，直线l：y=2x+2与抛物线y=2x2交于A、B两点，P为AB的中点，过P作x轴的垂线交抛物线于点C．
    （a）求A、B两点的坐标及C点的坐标；
    （b）连结AB、AC，求证△ABC为直角三角形；
    （c）将直线l平移到C点时得到直线l′，求两直线l与l′的距离．

    查看答案和解析>>

    同步练习册答案