
 阅读材料:
阅读材料:分析 (1)根据两点间的距离公式可得EF=$\sqrt{(0-6)^{2}+(2-10)^{2}}$=10,设M(x,y),则EM+FM=$\sqrt{{x^2}+{{({y-2})}^2}}+\sqrt{{{({x-6})}^2}+{{({y-10})}^2}}$,判断出当点M在E,F之间,且点E,M,F三点在一条直线上时,EM+FM=$\sqrt{{x^2}+{{({y-2})}^2}}+\sqrt{{{({x-6})}^2}+{{({y-10})}^2}}$有最小值即可得到结论;
(2)把点C,E坐标代入抛物线的解析式y=a(x-0)2+1中,则结论可得;
(3)①D是上述抛物线上的点,且其横坐标为-3,求出D(-3,$\frac{13}{4}$),代入两点间的距离公式即可得到DF=$\sqrt{(0+3)^{2}+(2-\frac{13}{4})^{2}}$=$\frac{13}{4}$;
②相等,由点P是该抛物线上的任意一点,设点P的坐标为(a,$\frac{1}{4}$a2+1),代入两点间的距离公式即可得到线段FP的长度与点P纵坐标相等;
③到定点的距离等于到定直线的距离的点的集合.
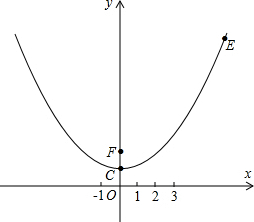
解答 解:(1)∵E(6,10),F(0,2),
∴EF=$\sqrt{(0-6)^{2}+(2-10)^{2}}$=10,
设M(x,y),则EM+FM=$\sqrt{{x^2}+{{({y-2})}^2}}+\sqrt{{{({x-6})}^2}+{{({y-10})}^2}}$,
当点M在E,F之间,且点E,M,F三点在一条直线上时,EM+FM=$\sqrt{{x^2}+{{({y-2})}^2}}+\sqrt{{{({x-6})}^2}+{{({y-10})}^2}}$有最小值,
EM+FM=$\sqrt{{x^2}+{{({y-2})}^2}}+\sqrt{{{({x-6})}^2}+{{({y-10})}^2}}$的最小值=EF=10,
故答案为:10,10;
(2)设以C为顶点,且经过点E的抛物线的解析式为:y=a(x-0)2+1,
∴10=36a+1,
∴a=$\frac{1}{4}$,
∴以C为顶点,且经过点E的抛物线的解析式为:y=$\frac{1}{4}$x2+1;
(3)①∵D是上述抛物线上的点,且其横坐标为-3,
∴y=$\frac{1}{4}$×9+1=$\frac{13}{4}$,
∴D(-3,$\frac{13}{4}$),
∴DF=$\sqrt{(0+3)^{2}+(2-\frac{13}{4})^{2}}$=$\frac{13}{4}$;
②相等,理由如下:
∵点P是该抛物线上的任意一点,
∴设点P的坐标为(a,$\frac{1}{4}$a2+1),
∴FP=$\sqrt{(a-0)^{2}+(\frac{1}{4}{a}^{2}+1-2)^{2}}$=$\sqrt{\frac{1}{16}{a}^{4}+\frac{1}{2}{a}^{2}+1}$=$\sqrt{(\frac{1}{4}{a}^{2}+1)^{2}}$=$\frac{1}{4}$a2+1;
∴线段FP的长度与点P纵坐标相等.
③到定点的距离等于到定直线的距离的点的集合.
故答案为:到定点的距离等于到定直线的距离的点的集合.
点评 本题考查了待定系数法求二次函数的解析式,两点间的距离公式,根据题意会应用两点间的距离公式解决问题是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
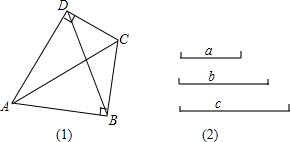 定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做损矩形的直径.
定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做损矩形的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 手机用户序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 发送短信息条数 | 20 | 19 | 20 | 20 | 21 | 17 | 15 | 23 | 20 | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com