
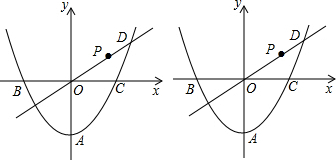
分析 (1)根据待定系数法求得即可;
(2)求得OB=OC=OP=2,从而求得∠APO=$∠BPO=\frac{45°}{2}$,即可求得∠APB=45°;
(3)求得PD∥AC,使得以A、C、D、P为顶点的四边形为平行四边形,则AC=PD=2$\sqrt{2}$,过P作PG⊥x轴于G,DH⊥x轴于H,通过三角形相似对应边成比例即可求得;
(4)先证得△AOB是等腰直角三角形,证得OE垂直平分AB,进而证得PB是∠ABO的平分线得出PE=PF,设PF=PE=OF=x,在RT△OPF中,根据勾股定理即可求得;
解答  解;(1)设抛物线的解析式为y=ax2+bx+c,
解;(1)设抛物线的解析式为y=ax2+bx+c,
∵抛物线与y轴交于A(0,-2),与x轴交于B(-2,0),C(2,0),
∴$\left\{\begin{array}{l}{c=-2}\\{4a-2b+c=0}\\{4a+2b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=0}\\{c=-2}\end{array}\right.$.
∴抛物线的解析式为y=$\frac{1}{2}$x2-2;
解$\left\{\begin{array}{l}{y=\frac{1}{2}{x}^{2}-2}\\{y=x}\end{array}\right.$得$\left\{\begin{array}{l}{x=1+\sqrt{5}}\\{y=1+\sqrt{5}}\end{array}\right.$或$\left\{\begin{array}{l}{x=1-\sqrt{5}}\\{y=1-\sqrt{5}}\end{array}\right.$,
∴D(1+$\sqrt{5}$,1+$\sqrt{5}$);
(2)如图1,把点P的横坐标为$\sqrt{2}$代入y=x得,y=x=$\sqrt{2}$,
∴P($\sqrt{2}$,$\sqrt{2}$),
∴OP=$\sqrt{2×(\sqrt{2})^{2}}$=2,
∵OB=OC=2,
∴OB=OC=OP=2,
∵∠POC=45°,
∴∠POA=90°+45°=135°,
∴∠APO=(180°-135°)×$\frac{1}{2}$=$\frac{45°}{2}$,
∴$∠BPO=\frac{45°}{2}$,
∴∠APB=45°;
(3)存在;
∵A(0,-2),C(2,0),
∴直线AC的解析式为y=x-2,
∴与直线y=x平行,
∵AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=2$\sqrt{2}$,
∴PD=2$\sqrt{2}$,
解$\left\{\begin{array}{l}{y=\frac{1}{2}{x}^{2}-2}\\{y=x}\end{array}\right.$得$\left\{\begin{array}{l}{x=1+\sqrt{5}}\\{y=1+\sqrt{5}}\end{array}\right.$或$\left\{\begin{array}{l}{x=1-\sqrt{5}}\\{y=1-\sqrt{5}}\end{array}\right.$,
∴D(1+$\sqrt{5}$,1+$\sqrt{5}$)
∴OD=$\sqrt{2}$+$\sqrt{10}$,
∴OP=OD-PD=$\sqrt{10}$-$\sqrt{2}$或OP=OD+PD=$\sqrt{10}$+3$\sqrt{2}$,
过P作PG⊥x轴于G,DH⊥x轴于H,
∴PG∥DH,
∴△POG∽△DOH,
∴$\frac{OG}{OP}$=$\frac{OH}{OD}$=$\frac{\sqrt{2}}{2}$,
即$\frac{OG}{\sqrt{10}-\sqrt{2}}$=$\frac{\sqrt{2}}{2}$或$\frac{OG}{\sqrt{10}+3\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
解得OG=$\sqrt{5}$-1或$\sqrt{5}$+3,
∴P的横坐标为$\sqrt{5}$-1或$\sqrt{5}$+3,
∵P的是直线y=x上的点,横坐标和纵坐标相等,
∴P的坐标为($\sqrt{5}$-1,$\sqrt{5}$-1)或($\sqrt{5}$+3,$\sqrt{5}$+3); (4)如图2,∵B(-2,0),C(2,0),
(4)如图2,∵B(-2,0),C(2,0),
∴OB=OC=2,
∴△ABO是等腰直角三角形,
∴∠ABO=∠BAO=45°,
∵点P是直线y=x上的点,
∴∠POB=∠POA,
∴OE⊥AB,BE=AE,
∴PB=PA,
∴∠PAB=∠PBA,
∵∠APB=135°,
∴∠PAB=∠PBA=22.5°
∴BP是∠ABO的平分线,
作PF⊥x轴于F,
∴PF=PE,
设PF=PE=OF=x,
∵OE垂直平分AB,∠AOB=90°,
∴OE=$\frac{1}{2}$AB=$\frac{1}{2}$×$2\sqrt{2}$=$\sqrt{2}$,
∴OP=$\sqrt{2}$-x,
在RT△OPF中,OP2=PF2+OF2,
即($\sqrt{2}$-x)2=x2+x2.
解得x1=2-$\sqrt{2}$,x2=-2-$\sqrt{2}$(舍去),
∴P(-2+$\sqrt{2}$,-2+$\sqrt{2}$).
点评 本题是二次函数的综合题,考查了待定系数法求二次函数的解析式,勾股定理的应用,三角形相似的判定和性质,角的平分线的性质等,熟练掌握性质定理是解题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读材料:
阅读材料:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
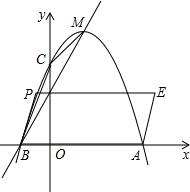 已知抛物线y=-x2+ax+b的顶点M(1,4),与x轴的一个交点A(3,0).
已知抛物线y=-x2+ax+b的顶点M(1,4),与x轴的一个交点A(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com