
【题目】如图1,△ABC和△DEF是两块可完全重合的三角板,![]() ,
,![]() .在如图1所示的状态下,△DEF固定不动,将△ABC沿直线a向左平移.
.在如图1所示的状态下,△DEF固定不动,将△ABC沿直线a向左平移.

(1)当△ABC移到图2位置时,连解AF、DC,求证:AF=DC;
(2)若EF=8,在上述平移过程中,试猜想点C距点E多远时,线段AD被直线a垂直平分。并证明你的猜想是正确的。
【答案】(1)见解析;(2)当点C距点E的距离为4时,理由见解析.
【解析】
(1)连接AF,CD,由BC=EF,得到BF=CE,证明△ABF≌△DEC,得到AF=DC.
(2)当点C距点E的距离为4时,线段AD被直线a垂直平分,利用直角三角形的性质,进行解答即可.
(1)如图2,连接AF,CD,
∵BC=EF,
∴BC-FC=EF-FC,
即BF=CE,
在△ABF和△DEC中,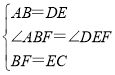 ,
,
∴△ABF≌△DEC,
∴AF=DC.
(2)当点C距点E的距离为4时,线段AD被直线a垂直平分,
证明:如图3,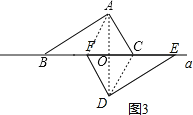
∵AF=DC,AC=DF,
∴四边形AFDC是平行四边形,
若AD被直线a垂直平分,假设a与AD交于点O,
在Rt△EFD中,∠DEF=30°
∴DF=![]() EF=4,
EF=4,
在Rt△FDO中,∠FDO=30°,
∴OF=![]() DF=2,
DF=2,
∴OC=2,
∴CE=EF-OF-OC=8-2-2=4.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,∠OAB=30°.
(Ⅰ)若点C在y轴上,且△ABC为以AB为腰的等腰三角形,求∠BCA的度数;
(Ⅱ)若B(1,0),沿AB将△ABO翻折至△ABD.请根据题意补全图形,并求点D的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE中,AB=AD=6,BC=DE,∠B=∠D=30°,边AD与边BC交于点P(不与点B,C重合),点B,E在AD异侧,I为△APC的内心.
(1)求证:∠BAD=∠CAE;
(2)设AP=x,请用含x的式子表示PD,并求PD的最大值;
(3)当AB⊥AC时,∠AIC的取值范围为m°<∠AIC<n°,分别直接写出m,n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
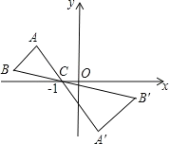
【题目】如图,△ABC中,A、B两个顶点在![]() 轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=![]() ,tan∠BA3C=
,tan∠BA3C=![]() ,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若A的对应点A2的坐标为(0,4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于(2,0)、(1,0),与y轴交于C,直线l1经过点C且平行于x轴,与抛物线的另一个交点为D,将直线l1向下平移t个单位得到直线l2,l2与抛物线交于A、B两点.
x2+bx+c与x轴交于(2,0)、(1,0),与y轴交于C,直线l1经过点C且平行于x轴,与抛物线的另一个交点为D,将直线l1向下平移t个单位得到直线l2,l2与抛物线交于A、B两点.


(1)求抛物线解析式及点C的坐标;
(2)当t=2时,探究△ABC的形状,并说明理由;
(3)在(2)的条件下,点M(m,0)在x轴上自由运动,过M作MN⊥x轴,交直线BC于P,交抛物线于N,若三个点M、N、P中恰有一个点是其他两个点连线段的中点(三点重合除外),则称M、N、P三点为“共谐点”,请直接写出使得M、P、N三点为“共谐点”的m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com