
【题目】如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,∠OAB=30°.
(Ⅰ)若点C在y轴上,且△ABC为以AB为腰的等腰三角形,求∠BCA的度数;
(Ⅱ)若B(1,0),沿AB将△ABO翻折至△ABD.请根据题意补全图形,并求点D的横坐标.

【答案】(Ⅰ)30°或75°或15°;(Ⅱ)![]() .
.
【解析】
(Ⅰ)根据等腰三角形的性质求角的度数,分点C在y轴的正负半轴两种情况求解即可;
(Ⅱ)通过题意补全图形后根据翻折和直角三角形30°角的性质即可求解.
解:(Ⅰ)如图:
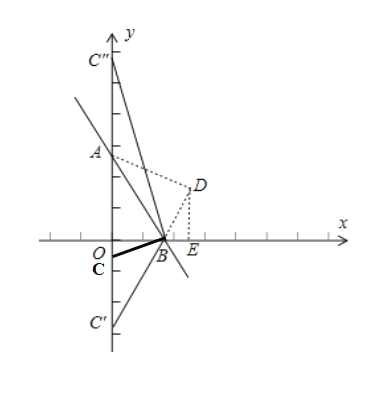
∵∠OAB=30°,当点C在y负半轴上时,△ABC为以AB为腰的等腰三角形,
如上图示,(1)当![]() 时,
时,
∴![]() ;
;
(2)当![]() 时,
时,
∴![]()
当点C在y轴正半轴上时,AB=AC″,
∴![]() ,
,
答:∠BCA的度数为30°或75°或15°.
(Ⅱ)如图:
沿AB将△ABO翻折至△ABD,过D点作DE⊥x轴于点E,
∵B(1,0),∴BD=OB=1,
∵∠OBA=∠DBA=60°,
∴∠DBE=60°,
∴∠BDE=30°,
∴BE=![]() DB=
DB=![]() ,
,
∴OE=OB+BE=![]() .
.
答:点D的横坐标为![]() .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形。用A种纸片张,B种纸片一张,C种纸片两张可拼成如图2的大正方形.

(1)请用两种不同的方法求图2大正方形的面积(答案直接填写到题中横线上);
方法1____________;方法2_____________;
(2)观察图2,请你直接写出下列三个代数式: (a+b)![]() , a
, a![]() +b
+b![]() ,ab之间的等量关系_____________;
,ab之间的等量关系_____________;
(3)类似的,请你用图1中的三种纸片拼一个图形验证:(a+b)(a+2b)=a![]() +3ab+2b
+3ab+2b![]() ;
;
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=6, a![]() +b
+b![]() =14,求ab的值;
=14,求ab的值;
②已知(x2018)![]() +(x2020)
+(x2020)![]() =34,求(x2019)
=34,求(x2019)![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,点
,点![]() 从点
从点![]() 出发以
出发以![]() 个单位
个单位![]() 的速度沿着线段
的速度沿着线段![]() 向终点
向终点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发也以
出发也以![]() 个单位
个单位![]() 的速度沿着线段
的速度沿着线段![]() 向终点
向终点![]() 运动,设运动时间为
运动,设运动时间为![]() .
.
![]() 填空:当
填空:当![]() 时,
时,![]() ________;
________;
![]() 当
当![]() 平分
平分![]() 时,直线
时,直线![]() 将菱形的周长分成两部分,求这两部分的比;
将菱形的周长分成两部分,求这两部分的比;
![]() 以
以![]() 为圆心,
为圆心,![]() 长为半径的
长为半径的![]() 是否能与直线
是否能与直线![]() 相切?如果能,求此时
相切?如果能,求此时![]() 的值;如果不能,说明理由.
的值;如果不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BD、CE分别是△ABC的AC边、AB边上的高,M是BC边的中点,分别连结MD、ME、DE。

(1)当∠BAC<90°时,垂足D、E分别落在边AC、AB上,如图1,求证:DM=EM;
(2)若∠BAC=120°,试判断△DEM的形状,并说明理由;
(3)当∠BAC= 时,△DEM是等腰直角三角形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F
(1) 说明BE=CF的理由
(2) 如果AB=a,AC=b,求AE、BE的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
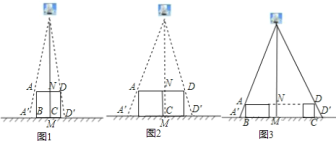
![]() 如图
如图![]() ,垂直于地面放置的正方形框架
,垂直于地面放置的正方形框架![]() ,边长
,边长![]() 为
为![]() ,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子
,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子![]() ,
,![]() 的长度和为
的长度和为![]() .那么灯泡离地面的高度为________.
.那么灯泡离地面的高度为________.
![]() 不改变图
不改变图![]() 中灯泡的高度,将两个边长为
中灯泡的高度,将两个边长为![]() 的正方形框架按图
的正方形框架按图![]() 摆放,请计算此时横向影子
摆放,请计算此时横向影子![]() ,
,![]() 的长度和为多少?
的长度和为多少?
![]() 有
有![]() 个边长为
个边长为![]() 的正方形按图
的正方形按图![]() 摆放,测得横向影子
摆放,测得横向影子![]() ,
,![]() 的长度和为
的长度和为![]() ,求灯泡离地面的距离.(写出解题过程,结果用含
,求灯泡离地面的距离.(写出解题过程,结果用含![]() ,
,![]() ,
,![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图形的变换趣味无穷,如图①,在平面直角坐标系中,线段l位于第二象限,A(a,b)是线段l上一点,对于线段我们也可以做一些变换:
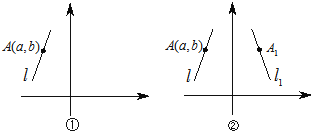
(1)如图②,将线段l以y轴为对称轴作轴对称变换得到线段l1,若点A(![]() ,3),则点A(
,3),则点A(![]() ,3)关于y轴为对称轴的点A1的坐标是______.
,3)关于y轴为对称轴的点A1的坐标是______.
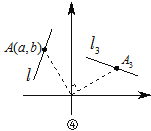
(2)如图④,将线段l绕坐标原点O顺时针方向旋转90°得到线段l2,则点A(a,b)对应的点A3的坐标是什么?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△DEF是两块可完全重合的三角板,![]() ,
,![]() .在如图1所示的状态下,△DEF固定不动,将△ABC沿直线a向左平移.
.在如图1所示的状态下,△DEF固定不动,将△ABC沿直线a向左平移.

(1)当△ABC移到图2位置时,连解AF、DC,求证:AF=DC;
(2)若EF=8,在上述平移过程中,试猜想点C距点E多远时,线段AD被直线a垂直平分。并证明你的猜想是正确的。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com