
【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
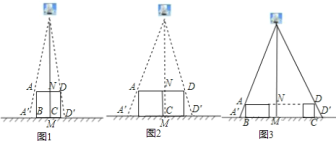
![]() 如图
如图![]() ,垂直于地面放置的正方形框架
,垂直于地面放置的正方形框架![]() ,边长
,边长![]() 为
为![]() ,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子
,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子![]() ,
,![]() 的长度和为
的长度和为![]() .那么灯泡离地面的高度为________.
.那么灯泡离地面的高度为________.
![]() 不改变图
不改变图![]() 中灯泡的高度,将两个边长为
中灯泡的高度,将两个边长为![]() 的正方形框架按图
的正方形框架按图![]() 摆放,请计算此时横向影子
摆放,请计算此时横向影子![]() ,
,![]() 的长度和为多少?
的长度和为多少?
![]() 有
有![]() 个边长为
个边长为![]() 的正方形按图
的正方形按图![]() 摆放,测得横向影子
摆放,测得横向影子![]() ,
,![]() 的长度和为
的长度和为![]() ,求灯泡离地面的距离.(写出解题过程,结果用含
,求灯泡离地面的距离.(写出解题过程,结果用含![]() ,
,![]() ,
,![]() 的代数式表示)
的代数式表示)
【答案】(1)180cm;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设灯泡的位置为点P,易得△PAD∽△PA′D′,设出所求的未知数,利用相似三角形的对应边的比等于对应高的比,可得灯泡离地面的高度;
(2)同法可得到横向影子A′B,D′C的长度和;
(3)按照相应的三角形相似,利用相似三角形的对应边的比等于对应高的比,用字母表示出其他线段,即可得到灯泡离地面的距离.
![]() 设灯泡离地面的高度为
设灯泡离地面的高度为![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
根据相似三角形对应高的比等于相似比的性质,可得![]() ,
,
∴![]() ,
,
解得![]() ,
,
故答案为:180cm;
![]() 设横向影子
设横向影子![]() ,
,![]() 的长度和为
的长度和为![]() ,
,
同理可得∴![]() ,
,
解得![]() ;
;
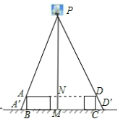
![]() 记灯泡为点
记灯泡为点![]() ,如图:
,如图:
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,
,
根据相似三角形对应高的比等于相似比的性质,可得![]() ,
,
设灯泡离地面距离为![]() ,由题意,得
,由题意,得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=-2x+4交x轴和y轴于点A和点B,点C(0,-2)在y轴上,连接AC。
(1)求点A和点B的坐标;
(2)若点P是直线AB上一点,若△APC的面积为4,求点P;
(3)过点B的直线BH交x轴于点H(H点在点A右侧),当∠ABE=45时,求直线BE。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于![]() AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
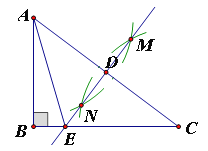
(1)∠ADE= °;
(2)AE CE(填“>、<、=”)
(3)当AB=3、AC=5时,△ABE的周长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,∠OAB=30°.
(Ⅰ)若点C在y轴上,且△ABC为以AB为腰的等腰三角形,求∠BCA的度数;
(Ⅱ)若B(1,0),沿AB将△ABO翻折至△ABD.请根据题意补全图形,并求点D的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】测量物体高度
![]() 小明想测量一棵树的高度
小明想测量一棵树的高度![]() ,在阳光下,小明测得一根长为
,在阳光下,小明测得一根长为![]() 米的竹竿的影长为
米的竹竿的影长为![]() 米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为
米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为![]() 米,落在地面上的影长为
米,落在地面上的影长为![]() 米,则树高
米,则树高![]() 为多少米.
为多少米.
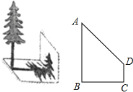
![]() 小明在某一时刻测得
小明在某一时刻测得![]() 的杆子在阳光下的影子长为
的杆子在阳光下的影子长为![]() ,他想测量电线杆
,他想测量电线杆![]() 的高度,但其影子恰好落在土坡的坡面
的高度,但其影子恰好落在土坡的坡面![]() 和地面
和地面![]() 上,量得
上,量得![]() ,
,![]() ,
,![]() 与地面成
与地面成![]() .
.
求电线杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD//BC,∠A=90°,E为AB上一点,且AE=BC,∠1=∠2.
请说明:(1)△ADE与△BEC全等吗?请说明理由;
(2)判断△CDE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋节是我国的传统节日,人们素有吃月饼的习俗.某超市在中秋节来临之际用3000元购进A、B两种月饼1100个,若购买A种月饼与购买B种月饼的费用相同,且A种月饼的单价是B种月饼单价的1.2倍.
(1)求A、B两种月饼的单价各是多少?
(2)若计划用不超过7000元的资金再次购进A、B两种月饼共2600个,已知A、B两种月饼的进价不变.求A种月饼最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=![]() ,tan∠BA3C=
,tan∠BA3C=![]() ,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com