
【题目】如图,直线y=-2x+4交x轴和y轴于点A和点B,点C(0,-2)在y轴上,连接AC。
(1)求点A和点B的坐标;
(2)若点P是直线AB上一点,若△APC的面积为4,求点P;
(3)过点B的直线BH交x轴于点H(H点在点A右侧),当∠ABE=45时,求直线BE。

【答案】(1)A(2,0),B(0,4)(2)![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,-
,-![]() )(3)
)(3)![]()
【解析】
(1)根据x轴上的点的纵坐标为0,y轴上的点的横坐标为0即可求出点A、B的坐标;(2)分三种情况,当点P在x轴上方(即在点A、B之间)时,![]() ;当点P在x轴下方时,则
;当点P在x轴下方时,则![]() 进行计算;因为
进行计算;因为![]() =4,所以点P不会在点B的上方;(3)过点A作AD⊥AB交BE于点D,过点D作DH⊥X轴 ,由∠ABE=45
=4,所以点P不会在点B的上方;(3)过点A作AD⊥AB交BE于点D,过点D作DH⊥X轴 ,由∠ABE=45
可得△BAD为等腰直角三角形,易证△AOB≌△DHA ,又因为OA=2,OB=4所以OH=4,DH=2,所以D(6,2),已知B(0,4) ,利用待定系数法可得 ![]() .
.
(1)∵y=-2x+4交X轴和y轴于点A和点B
∴当x=0时,y=4;
当y=0时,x=2
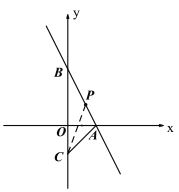
∴A(2,0),B(0,4)
(2) 设点P(a,-2a+4)
①如图,当点P在x轴上方时,
则![]()
∴4=![]()
∴a=![]()
∴![]() (
(![]() ,
,![]() )
)
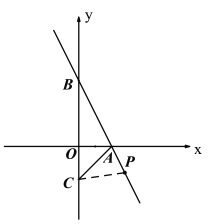
②如图,当点P在x轴下方时
则![]()
∴4=![]()
∴a=![]()
∴![]() (
(![]() ,-
,-![]() )
)
③因为![]() =4,所以点P不会在点B的上方;
=4,所以点P不会在点B的上方;
(3)当∠ABE=45,设直线BE:y=kx+b
如图, 过点A作AD⊥AB交BE于点D,过点D作DH⊥X轴
∵∠ABE=45
∴△BAD为等腰直角三角形,
易证△AOB≌△DHA
∵OA=2,OB=4
∴OH=4,DH=2
∴D(6,2)
∵B(0,4)
∴![]()


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解答下列问题:
在形如ab=N的式子中,我们已经研究过两种情况:
①已知a和b,求N,这是乘方运算;
②已知b和N,求a,这是开方运算.
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫作对数运算.
定义:如果ab=N(a>0.a≠1,N>0),则b叫作以a为底的N的对数,记作b=logaN.
例如:因为23=8,所以log28=3;因为![]() ,所以
,所以![]() .
.
(1)根据定义计算:
①log381= ; ②log33= ;
③log31= ; ④如果logx16=4,那么x= .
(2)设ax=M,ay=N,则logaN=y(a>0,a≠1,M、N均为正数).用logaM,logaN的代数式分别表示logaMN及![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 与一次函数y=x+b的图象交于A(1,-k+4),B(k-4,-1)两点.
与一次函数y=x+b的图象交于A(1,-k+4),B(k-4,-1)两点.
(1)试确定这两个函数的表达式;
(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形。用A种纸片张,B种纸片一张,C种纸片两张可拼成如图2的大正方形.

(1)请用两种不同的方法求图2大正方形的面积(答案直接填写到题中横线上);
方法1____________;方法2_____________;
(2)观察图2,请你直接写出下列三个代数式: (a+b)![]() , a
, a![]() +b
+b![]() ,ab之间的等量关系_____________;
,ab之间的等量关系_____________;
(3)类似的,请你用图1中的三种纸片拼一个图形验证:(a+b)(a+2b)=a![]() +3ab+2b
+3ab+2b![]() ;
;
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=6, a![]() +b
+b![]() =14,求ab的值;
=14,求ab的值;
②已知(x2018)![]() +(x2020)
+(x2020)![]() =34,求(x2019)
=34,求(x2019)![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
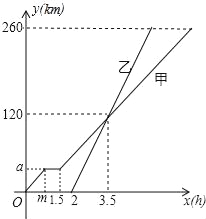
【题目】甲、乙两车从A地匀速驶向B地,甲车比乙车早出发2小时,并且甲车图中休息了0.5小时后仍以原速度驶向B地,如图是甲、乙两车行驶的路程y(千米)与行驶的时间x(小时)之间的函数图象.下列说法:
①m=1,a=40;
②甲车的速度是40千米/小时,乙车的速度是80千米/小时;
③当甲车距离A地260千米时,甲车所用的时间为7小时;
④当两车相距20千米时,则乙车行驶了3或4小时,
其中正确的个数是( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
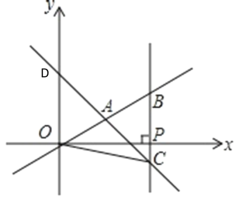
【题目】在平面直角坐标系xOy中,一次函数y=x+m的图象交y轴于点D,且它与正比例函数![]() 的图象交于点A(2,n),设x轴上有一点P,过点P作x轴的垂线(垂线位于点A的右侧),分别交
的图象交于点A(2,n),设x轴上有一点P,过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和y=x+m的图象与点B、C.
和y=x+m的图象与点B、C.
(1)求m和n的值;
(2)若BC=OD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,点
,点![]() 从点
从点![]() 出发以
出发以![]() 个单位
个单位![]() 的速度沿着线段
的速度沿着线段![]() 向终点
向终点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发也以
出发也以![]() 个单位
个单位![]() 的速度沿着线段
的速度沿着线段![]() 向终点
向终点![]() 运动,设运动时间为
运动,设运动时间为![]() .
.
![]() 填空:当
填空:当![]() 时,
时,![]() ________;
________;
![]() 当
当![]() 平分
平分![]() 时,直线
时,直线![]() 将菱形的周长分成两部分,求这两部分的比;
将菱形的周长分成两部分,求这两部分的比;
![]() 以
以![]() 为圆心,
为圆心,![]() 长为半径的
长为半径的![]() 是否能与直线
是否能与直线![]() 相切?如果能,求此时
相切?如果能,求此时![]() 的值;如果不能,说明理由.
的值;如果不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
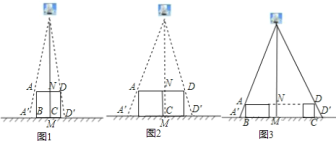
![]() 如图
如图![]() ,垂直于地面放置的正方形框架
,垂直于地面放置的正方形框架![]() ,边长
,边长![]() 为
为![]() ,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子
,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子![]() ,
,![]() 的长度和为
的长度和为![]() .那么灯泡离地面的高度为________.
.那么灯泡离地面的高度为________.
![]() 不改变图
不改变图![]() 中灯泡的高度,将两个边长为
中灯泡的高度,将两个边长为![]() 的正方形框架按图
的正方形框架按图![]() 摆放,请计算此时横向影子
摆放,请计算此时横向影子![]() ,
,![]() 的长度和为多少?
的长度和为多少?
![]() 有
有![]() 个边长为
个边长为![]() 的正方形按图
的正方形按图![]() 摆放,测得横向影子
摆放,测得横向影子![]() ,
,![]() 的长度和为
的长度和为![]() ,求灯泡离地面的距离.(写出解题过程,结果用含
,求灯泡离地面的距离.(写出解题过程,结果用含![]() ,
,![]() ,
,![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com