
【题目】在平面直角坐标系xOy中,一次函数y=x+m的图象交y轴于点D,且它与正比例函数![]() 的图象交于点A(2,n),设x轴上有一点P,过点P作x轴的垂线(垂线位于点A的右侧),分别交
的图象交于点A(2,n),设x轴上有一点P,过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和y=x+m的图象与点B、C.
和y=x+m的图象与点B、C.
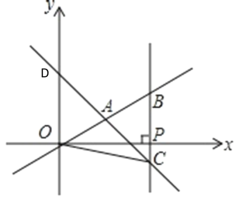
(1)求m和n的值;
(2)若BC=OD,求点P的坐标.
【答案】(1)m=3,![]() ;(2)(4,0)
;(2)(4,0)
【解析】
(1)将A(2,n)代入![]() 中即可求出n,然后再将A代入y=x+m即可求出m;
中即可求出n,然后再将A代入y=x+m即可求出m;
(2)设P点坐标为(a,0),然后分别表示出B、C两点的坐标,即可表示出BC的长,然后根据BC=OD列方程即可.
解:(1)将A(2,n)代入![]() 中,得:
中,得:
![]() ,
,
再将A(2,1)代入y=x+m中,得:
1=2+m
解得:m=3
(2)设P点坐标为(a,0)
∵过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和y=x+3的图象与点B、C
和y=x+3的图象与点B、C
∴点B的坐标为![]() ,点C的坐标为:
,点C的坐标为:![]()
∴BC=![]()
把x=0代入y=x+3中,解得y=3
故点D的坐标为(0,3)
∴OD=3
∵BC=OD
∴![]()
解得:![]()
∴P点坐标为(4,0)


科目:初中数学 来源: 题型:
【题目】已知直线![]() 与
与![]() 交于A,B两点,且点A的横坐标为4,过原点O的另一条直线l交双曲线
交于A,B两点,且点A的横坐标为4,过原点O的另一条直线l交双曲线![]() 于P,Q两点(点P在第一象限),由点A,B,P,Q为顶点组成的四边形面积为24,则点P的坐标为_________.
于P,Q两点(点P在第一象限),由点A,B,P,Q为顶点组成的四边形面积为24,则点P的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某加工企业生产并销售某种农产品,假设销售量与加工产量相等.已知每千克生产成本y1(单位:元)与产量x(单位:kg)之间满足表达式y1=![]() 下图中线段AB表示每千克销售价格y2(单位:元)与产量x(单位:kg)之间的函数表达式.
下图中线段AB表示每千克销售价格y2(单位:元)与产量x(单位:kg)之间的函数表达式.
(1)试确定每千克销售价格y2与产量x之间的函数表达式,并写出自变量的取值范围;
(2)若用w(单位:元)表示销售该农产品的利润,试确定w与产量x之间的函数表达式;
(3)求销售量为70 kg时,销售该农产品是赚钱,还是亏本?赚钱或亏本了多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
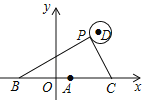
【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-2x+4交x轴和y轴于点A和点B,点C(0,-2)在y轴上,连接AC。
(1)求点A和点B的坐标;
(2)若点P是直线AB上一点,若△APC的面积为4,求点P;
(3)过点B的直线BH交x轴于点H(H点在点A右侧),当∠ABE=45时,求直线BE。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线L经过点A,BD⊥直线L,CE⊥直线L,垂足分别为点D、E.证明:DE=BD+CE.
(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线L上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图③,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高,延长HA交EG于点I,求证:I是EG的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为______.
周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形于1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示三角形的两条直角边(x>y),下列四个说法:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 。其中说法正确的是( )
。其中说法正确的是( )

A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD//BC,∠A=90°,E为AB上一点,且AE=BC,∠1=∠2.
请说明:(1)△ADE与△BEC全等吗?请说明理由;
(2)判断△CDE的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com