
【题目】甲、乙两车从A地匀速驶向B地,甲车比乙车早出发2小时,并且甲车图中休息了0.5小时后仍以原速度驶向B地,如图是甲、乙两车行驶的路程y(千米)与行驶的时间x(小时)之间的函数图象.下列说法:
①m=1,a=40;
②甲车的速度是40千米/小时,乙车的速度是80千米/小时;
③当甲车距离A地260千米时,甲车所用的时间为7小时;
④当两车相距20千米时,则乙车行驶了3或4小时,
其中正确的个数是( )
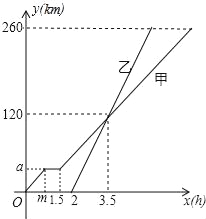
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
①观察图象找出点(3.5,120),根据“速度=路程÷行驶时间”可以算出甲车的速度,再结合甲车中途休息半个小时即可得出a、m的值;
②根据点(3.5,120),利用“速度=路程÷行驶时间”可以算出乙车的速度;
③根据“时间=路程÷速度”可算出甲车距离A地260千米时行驶的时间,加上休息的0.5小时即可得出结论;
④根据点(3.5,120),结合两车速度差即可算出当两车相距20千米时,甲车行驶的时间,再根据甲车比乙车早出发2小时可得出乙车行驶时间.
对比给定的说法即可得出结论.
①∵甲车途中休息了0.5小时,
∴m=1.5﹣0.5=1,
甲车的速度为:120÷(3.5﹣0.5)=40(千米/小时).
a=1×40=40.
∴①成立;
②乙车的速度为:120÷(3.5﹣2)=80(千米/时),
∴甲车的速度是40千米/小时,乙车的速度是80千米/小时,②成立;
③当甲车距离A地260千米时,甲车所用的时间为:260÷40+0.5=7(小时),
∴③成立;
④∵两车相遇时时间为3.5时,且甲车速度为40千米/时,乙车速度为80千米/时,
∴当两车相距20千米时,甲车行驶的时间为:3.5+20÷(80﹣40)=4(小时)或3.5﹣20÷(80﹣40)=3(小时),
又∵甲车比乙车早出发2小时,
∴当两车相距20千米时,则乙车行驶了1或2小时,④不正确.
综上可知:正确的结论有①②③.
故选:C.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,A(1,3),B(2,1),直角坐标系中存在点C,使得O,A,B,C四点构成平行四边形,则C点的坐标为______________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到边AB的距离为( )
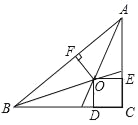
A. 2cmB. 3cmC. 4cmD. 5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+a﹣2=0
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程总有两个不相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,如果∠GFH与∠BHC互补.
(1)说明:∠1=∠2.
(2)若∠A=80°,FG⊥AC,求∠ACB的度数.
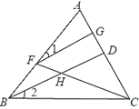
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于红星路济宁师专旧址的济宁学院附中红星校区将于近期开始动工,原计划在年内拆除旧校舍与建造新校舍共12万平方米,为建设一座园林式的校园,在实施中调整拆建计划,新建面积减少10%,拆除面积增加10%,结果拆除和新建总面积不变.根据协议,施工方免费拆除旧校舍,但建造新校舍每平米需要1500元,校园环境建设每平方米需要600元.
(1)求原计划拆、建的面积各多少平方米?
(2)若把实际的拆、建工程中节余的资金的30%用来增加校园环境建设,可建设多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.
(1)若BF⊥AE,
①求证:BF=AE;
②连接OD,确定OD与AB的数量关系,并证明;
(2)若正方形的边长为4,且BF=AE,求BO的长.
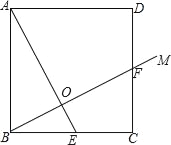
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y= ![]() x刻画.
x刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com