
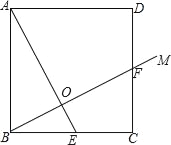
【题目】已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.
(1)若BF⊥AE,
①求证:BF=AE;
②连接OD,确定OD与AB的数量关系,并证明;
(2)若正方形的边长为4,且BF=AE,求BO的长.
【答案】(1)①见解析;②OD=AB.证明见解析;(2)①BO=![]() 或BO=
或BO=![]() .
.
【解析】
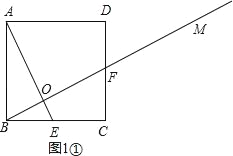
(1)①如图1①,要证BF=AE,只需证△ABE≌△BCF,只需证到∠BAE=∠CBF即可;
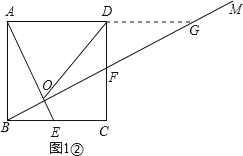
②延长AD,交射线BM于点G,如图1②,由△ABE≌△BCF可得BE=CF,由此可得CF=DF,从而可证到△DGF≌△CBF,则有DG=BC,从而可得DG=AD,然后运用直角三角形斜边上的中线等于斜边的一半即可解决问题;
(2)可分点F在CD上和点F在AD上两种情况进行讨论.当点F在CD上时,如图2①,易证Rt△ABE≌Rt△BCF(HL),则有∠BAE=∠CBF,由此可证到∠AOB=90°,然后在Rt△ABE中,运用面积法就可求出BO的长;当点F在AD上时,如图2②,易证Rt△ABE≌Rt△BAF(HL),则有∠BAE=∠ABF,根据等角对等边可得OB=OA,根据等角的余角相等可得∠AEB=∠EBF,根据等角对等边可得OB=OE,即可得到OA=OB=OE,只需求出AE的长就可解决问题.
(1)①如图1①,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABE=∠C=90°,
∴∠BAE+∠AEB=90°,
∵BF⊥AE,
∴∠CBF+∠AEB=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中,
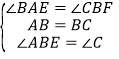 ,
,
∴△ABE≌△BCF(ASA),
∴BF=AE;
②OD=AB.
证明:延长AD,交射线BM于点G,如图1②,
∵△ABE≌△BCF,
∴BE=CF.
∵E为BC的中点,
∴CF=BE=![]() BC=
BC=![]() DC,
DC,
∴CF=DF.
∵DG∥BC,
∴∠DGF=∠CBF.
在△DGF和△CBF中,
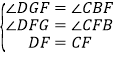 ,
,
∴△DGF≌△CBF,
∴DG=BC,
∴DG=AD.
∵BF⊥AE,
∴OD=![]() AG=AD=AB;
AG=AD=AB;
(2)①若点F在CD上,如图2①,

在Rt△ABE和Rt△BCF中,
![]() ,
,
∴Rt△ABE≌Rt△BCF(HL),
∴∠BAE=∠CBF,
∵∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,
∴∠AOB=90°.
∵∠ABE=90°,AB=4,BE=2,
∴AE=![]() =2
=2![]() .
.
∵S△ABE=![]() ABBE=
ABBE=![]() AEBO,
AEBO,
∴BO=![]() .
.
②若点F在AD上,如图2②,
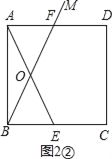
在Rt△ABE和Rt△BAF中,
![]() ,
,
∴Rt△ABE≌Rt△BAF(HL),
∴∠BAE=∠ABF,
∴OB=OA.
∵∠BAE+∠AEB=90°,∠ABF+∠EBF=90°,
∴∠AEB=∠EBF,
∴OB=OE,
∴OA=OB=OE.
∵∠ABE=90°,AB=4,BE=2,
∴AE=![]() =2
=2![]() ,
,
∴OB=![]() AE=
AE=![]() .
.
综上所述:BO的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】2017年怀柔区中考体育加试女子800米耐力测试中,同时起跑的李丽和吴梅所跑的路程![]() 米
米![]() 与所用时间
与所用时间![]() 秒
秒![]() 之间的函数图象分别为线段OA和折线
之间的函数图象分别为线段OA和折线![]() 下列说法正确的是
下列说法正确的是![]()
![]()
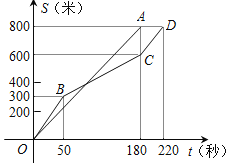
A. 李丽的速度随时间的增大而增大
B. 吴梅的平均速度比李丽的平均速度大
C. 在起跑后180秒时,两人相遇
D. 在起跑后50秒时,吴梅在李丽的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
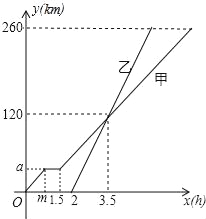
【题目】甲、乙两车从A地匀速驶向B地,甲车比乙车早出发2小时,并且甲车图中休息了0.5小时后仍以原速度驶向B地,如图是甲、乙两车行驶的路程y(千米)与行驶的时间x(小时)之间的函数图象.下列说法:
①m=1,a=40;
②甲车的速度是40千米/小时,乙车的速度是80千米/小时;
③当甲车距离A地260千米时,甲车所用的时间为7小时;
④当两车相距20千米时,则乙车行驶了3或4小时,
其中正确的个数是( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学骑自行车去郊外春游,骑行1小时后,自行车出现故障,维修好后继续骑行,下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的图象.
(1)根据图象回答:小明到达离家最远的地方用了多长时间?此时离家多远?
(2)求小明出发2.5小时后离家多远;
(3)求小明出发多长时间离家12千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=x2+bx+c经过点(2,-3)和(4,5).
(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图象G,求图象G的表达式;
(3)在(2)的条件下,当-2<x<2时,直线y=m与该图象有一个公共点,求m的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,若按图中规律继续下去,则∠1+∠2+…+∠n等于( )
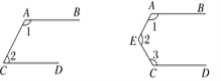

A. n·180° B. 2n·180° C. (n-1)·180° D. (n-1)2·180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:
①E为AB的中点;
②FC=4DF;
③S△ECF= ![]() ;
;
④当CE⊥BD时,△DFN是等腰三角形.
其中一定正确的是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
△ABC | A(a,0) | B(3,0) | C(5,5) |
△A1B1C1 | A1(﹣3,2) | B1(﹣1,b) | C1(c,7) |
(1)观察表中各对应点坐标的变化,并填空:a= ,b= ,c= ;
(2)在如图的平面直角坐标系中画出△ABC及△A1B1C1;
(3)△A1B1C1的面积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com