
【题目】已知关于x的方程x2+ax+a﹣2=0
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程总有两个不相等的实数根
【答案】
(1)解:把x=1代入方程, ![]() 所以a=
所以a= ![]() ,再代入方程,
,再代入方程,
![]() ,解得方程的另一个根为﹣
,解得方程的另一个根为﹣ ![]() .
.
(2)证明:∵△=a2﹣4(a﹣2)=a2﹣4a+8=a2﹣4a+4+4=(a﹣2)2+4>0,
∴不论a取何实数,该方程都有两个不相等的实数根.
【解析】(1)将x=1代入方程就可求出a的值,再将a的值代入方程,解方程即可求出方程的另一个根。或利用根与系数的关系求解。
(2)先求出b2-4ac的值,再说明b2-4ac>0即可。
【考点精析】利用求根公式和根与系数的关系对题目进行判断即可得到答案,需要熟知根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】阅读:
我们知道,![]() 于是要解不等式
于是要解不等式![]() ,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:
,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:
解:(1)当![]() ,即
,即![]() 时:
时:![]()
解这个不等式,得:![]()
由条件![]() ,有:
,有:![]()
(2)当![]() ,即
,即![]() 时,
时,![]()
解这个不等式,得:![]()
由条件![]() ,有:
,有:![]()
∴ 如图,![]()
综合(1)、(2)原不等式的解为:![]()
根据以上思想,请探究完成下列![]() 个小题:
个小题:
![]() ;
;
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=kx+b经过点A(﹣30,0)和点B(0,15),直线y=x+5与直线y=kx+b相交于点P,与y轴交于点C.

(1)求直线y=kx+b的解析式.
(2)求△PBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地匀速驶向B地,甲车比乙车早出发2小时,并且甲车图中休息了0.5小时后仍以原速度驶向B地,如图是甲、乙两车行驶的路程y(千米)与行驶的时间x(小时)之间的函数图象.下列说法:
①m=1,a=40;
②甲车的速度是40千米/小时,乙车的速度是80千米/小时;
③当甲车距离A地260千米时,甲车所用的时间为7小时;
④当两车相距20千米时,则乙车行驶了3或4小时,
其中正确的个数是( )
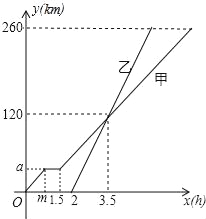
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).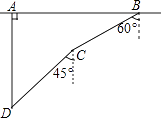
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学骑自行车去郊外春游,骑行1小时后,自行车出现故障,维修好后继续骑行,下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的图象.
(1)根据图象回答:小明到达离家最远的地方用了多长时间?此时离家多远?
(2)求小明出发2.5小时后离家多远;
(3)求小明出发多长时间离家12千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在《几何原本》中记载着这样的题目:如果同一条线段被两个分点先后分成相等和不相等的线段,以得到的各线段为边作正方形,那么不相等的两个正方形的面积之和等于原线段一半上的正方形与两个分点之间一段上正方形的面积之和的两倍.王老师带领学生在阅读的基础上画出的部分图形如图,已知线段![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上任意一点(
上任意一点(![]() 不与
不与![]() 重合),分别以
重合),分别以![]() 和
和![]() 为边在
为边在![]() 的下方作正方形
的下方作正方形![]() 和正方形
和正方形![]() ,以
,以![]() 和
和![]() 为边在线段下方作正方形
为边在线段下方作正方形![]() 和正方形
和正方形![]() ,则正方形
,则正方形![]() 与正方形
与正方形![]() 的面积之和等于正方形
的面积之和等于正方形![]() 和正方形
和正方形![]() 面积之和的两倍.
面积之和的两倍.
(1)请你画出正方形![]() 和正方形
和正方形![]() (不必尺规作图);
(不必尺规作图);
(2)设![]() ,
,![]() ,根据题意写出关于
,根据题意写出关于![]() 的等式并证明.
的等式并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com