
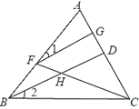
【题目】如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,如果∠GFH与∠BHC互补.
(1)说明:∠1=∠2.
(2)若∠A=80°,FG⊥AC,求∠ACB的度数.
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】学校“百变魔方”社团准备购买![]() 、
、![]() 两种魔方,已知购买
两种魔方,已知购买![]() 个
个![]() 种魔方和
种魔方和![]() 个
个![]() 种魔方共需
种魔方共需![]() 元,又知购买
元,又知购买![]() 个
个![]() 种魔方所需款数和购买
种魔方所需款数和购买![]() 个
个![]() 种魔方所需款数相同.
种魔方所需款数相同.
(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买![]() 、
、![]() 两种魔方共
两种魔方共![]() 个.某商店有两种优惠活动,如图所示。请根据以上信息,如何购买可以使两种优惠方案一致.
个.某商店有两种优惠活动,如图所示。请根据以上信息,如何购买可以使两种优惠方案一致.
⑶当购买![]() 种魔方
种魔方![]() 个时该如何花费才能使得所花钱数最少.
个时该如何花费才能使得所花钱数最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在ΔABC外的点![]() 处,若∠1=20°,则∠2的度数为( )
处,若∠1=20°,则∠2的度数为( )

A. 80°B. 90°
C. 100°D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
(1)(观察猜想)当点E在AB的中点时,如图1,过点E作EF∥BC,交AC于点F,观察猜想得到线段AE与DB的大小关系是 ;
(2)(探究证明)当点E不是AB的中点时,如图2,上述结论是否成立,如果成立,请写出解答过程,如果不成立,请说明理由;
(3)(拓展延伸)在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC,若△ABC的边长为2,AE=1,求CD的长(请直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
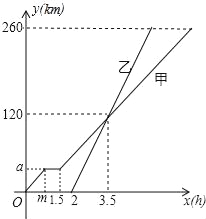
【题目】甲、乙两车从A地匀速驶向B地,甲车比乙车早出发2小时,并且甲车图中休息了0.5小时后仍以原速度驶向B地,如图是甲、乙两车行驶的路程y(千米)与行驶的时间x(小时)之间的函数图象.下列说法:
①m=1,a=40;
②甲车的速度是40千米/小时,乙车的速度是80千米/小时;
③当甲车距离A地260千米时,甲车所用的时间为7小时;
④当两车相距20千米时,则乙车行驶了3或4小时,
其中正确的个数是( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣ ![]() x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).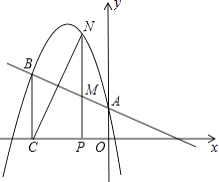
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=x2+bx+c经过点(2,-3)和(4,5).
(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图象G,求图象G的表达式;
(3)在(2)的条件下,当-2<x<2时,直线y=m与该图象有一个公共点,求m的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,同底数幂的乘法法则为:am·an=am+n(其中a≠0,m,n为正整数),类似地我们规定关于任意正整数m,n的一种新运算:h(m+n)=h(m)·h(n),请根据这种新运算填空:
(1)若h(1)=![]() ,则h(2)=________;
,则h(2)=________;
(2)若h(1)=k(k≠0),则h(n)·h(2017)=________(用含n和k的代数式表示,其中n为正整数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com