
����Ŀ����������߶�
![]() С�������һ�����ĸ߶�
С�������һ�����ĸ߶�![]() ���������£�С�����һ����Ϊ
���������£�С�����һ����Ϊ![]() ����͵�Ӱ��Ϊ
����͵�Ӱ��Ϊ![]() �ף�ͬʱ��һ��ͬѧ����һ�����ĸ߶�ʱ����������Ӱ�Ӳ�ȫ���ڵ����ϣ���һ����Ӱ�����ڽ�ѧ¥��ǽ���ϣ���ͼ������Ӱ��Ϊ
�ף�ͬʱ��һ��ͬѧ����һ�����ĸ߶�ʱ����������Ӱ�Ӳ�ȫ���ڵ����ϣ���һ����Ӱ�����ڽ�ѧ¥��ǽ���ϣ���ͼ������Ӱ��Ϊ![]() �ף����ڵ����ϵ�Ӱ��Ϊ
�ף����ڵ����ϵ�Ӱ��Ϊ![]() �ף�������
�ף�������![]() Ϊ�����ף�
Ϊ�����ף�
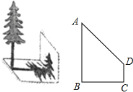
![]() С����ijһʱ�̲��
С����ijһʱ�̲��![]() �ĸ����������µ�Ӱ�ӳ�Ϊ
�ĸ����������µ�Ӱ�ӳ�Ϊ![]() ������������߸�
������������߸�![]() �ĸ߶ȣ�����Ӱ��ǡ���������µ�����
�ĸ߶ȣ�����Ӱ��ǡ���������µ�����![]() �͵���
�͵���![]() �ϣ�����
�ϣ�����![]() ��
��![]() ��
��![]() ������
������![]() ��
��
����߸˵ĸ߶ȣ�
���𰸡���1������Ϊ![]() �ף���2��
�ף���2��![]() ��
��
��������
��1����ͬһʱ����ߺ�Ӱ�������ȣ�����ͬһʱ�̵��������壬Ӱ�ӣ��������嶥����̫���������߹��ɵ�����ֱ�����������ƣ������У��������ڽ�ѧ¥�ϵ�Ӱ�ӵĶ��������Ĵ��ߺ;���������̫�������Լ������������Σ�����ͣ�Ӱ�ӹ����γɵ����������ƣ������Ϳ�������㵽���Ķ��˵ĸ߶ȣ��ټ���ǽ�ϵ�Ӱ�߾������ߣ�
��2���ȸ������⻭��ͼ�Σ���DE��BC��BC�ӳ�����E����DF��AB��F���ٸ���CD�ij��Լ��½��������б���ϵ�Ӱ������AF��Ӱ����Ȼ�����1 m�˵�Ӱ�ӳ�Ϊ2 m�������߸�AF�ĸ߶ȣ��ټ�DE�ij�����Ϊ���߸�AB�ĸ߶ȣ�
��1�����ǽ�ϵ�Ӱ�ӵĶ��˵����Ķ��˵Ĵ�ֱ�߶���x������
![]() ��
��
��ã�x=4��
��������AB=4+1.2=5.2���ף���
������Ϊ5.2����
![]() ��
��![]() ��
��![]() �ӳ�����
�ӳ�����![]() ����
����![]() ��
��![]() ��
��

�������֪��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�֡�ijһʱ�̲��![]() �ĸ����������µ�Ӱ�ӳ�Ϊ
�ĸ����������µ�Ӱ�ӳ�Ϊ![]() ��
��
��![]() ��
��
��![]() ��
��
���ı���![]() Ϊ���Σ�
����
��![]() ��
��
����߸˵ĸ߶�![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������A������ʻ��B�أ��׳����ҳ������2Сʱ�����Ҽ׳�ͼ����Ϣ��0.5Сʱ������ԭ�ٶ�ʻ��B�أ���ͼ�Ǽס���������ʻ��·��y��ǧ�ף�����ʻ��ʱ��x��Сʱ��֮��ĺ���ͼ������˵����
��m��1��a��40��
�ڼ׳����ٶ���40ǧ��/Сʱ���ҳ����ٶ���80ǧ��/Сʱ��
�۵��׳�����A��260ǧ��ʱ���׳����õ�ʱ��Ϊ7Сʱ��
�ܵ��������20ǧ��ʱ�����ҳ���ʻ��3��4Сʱ��
������ȷ�ĸ����ǣ�������
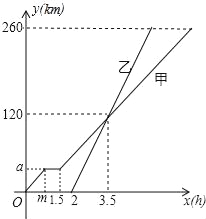
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �Ķ���
�Ķ���![]() ������ֱ�߷�������
������ֱ�߷�������![]() ���ϵ��������ɵı�
���ϵ��������ɵı�![]() ����������ֱ�߷�
����������ֱ�߷�![]() �����ɵı�
�����ɵı�![]() Ϊ�� ��
�� ��

A. 4:5:3 B. 3:4:2 C. 2:3:1 D. 1:1:1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪BD��CE�ֱ��ǡ�ABC��AC�ߡ�AB���ϵĸߣ�M��BC�ߵ��е㣬�ֱ�����MD��ME��DE��

��1������BAC<90��ʱ������D��E�ֱ����ڱ�AC��AB�ϣ���ͼ1����֤��DM=EM��
��2������BAC=120�������жϡ�DEM����״����˵�����ɣ�
��3������BAC= ʱ����DEM�ǵ���ֱ�������Ρ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ��
��![]() ��
��![]() ��Ҫ����
��Ҫ����![]() ��
��![]() ���صľ��룬�ס��ҡ�����������ͬѧ�ֱ�����˲����߶εij��ȺͽǵĶ������õ������������ݣ��ף�
���صľ��룬�ס��ҡ�����������ͬѧ�ֱ�����˲����߶εij��ȺͽǵĶ������õ������������ݣ��ף�![]() ��
��![]() ���ң�
���ң�![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() �����������
�����������![]() ��
��![]() ���ؾ�����У� ��
���ؾ�����У� ��

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ͼ�λͬѧ���ֵ�Ӱ����Ϸʱ�����ֶ���ͬһ���壬Ӱ�ӵĴ�С���Դ������ľ����йأ���ˣ�������Ϊ�����Խ��������Ӱ�ӳ��ȼ����Դ�������λ�ã����ǣ������������³��ԣ�
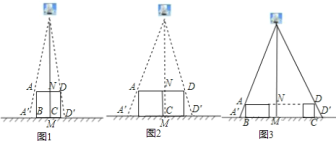
![]() ��ͼ
��ͼ![]() ����ֱ�ڵ�����õ������ο��
����ֱ�ڵ�����õ������ο��![]() ���߳�
���߳�![]() Ϊ
Ϊ![]() ���������Ϸ���һ���ݣ��ڵ��ݵ������£������ο�ܵĺ���Ӱ��
���������Ϸ���һ���ݣ��ڵ��ݵ������£������ο�ܵĺ���Ӱ��![]() ��
��![]() �ij��Ⱥ�Ϊ
�ij��Ⱥ�Ϊ![]() ����ô���������ĸ߶�Ϊ________��
����ô���������ĸ߶�Ϊ________��
![]() ���ı�ͼ
���ı�ͼ![]() �е��ݵĸ߶ȣ��������߳�Ϊ
�е��ݵĸ߶ȣ��������߳�Ϊ![]() �������ο�ܰ�ͼ
�������ο�ܰ�ͼ![]() �ڷţ�������ʱ����Ӱ��
�ڷţ�������ʱ����Ӱ��![]() ��
��![]() �ij��Ⱥ�Ϊ���٣�
�ij��Ⱥ�Ϊ���٣�
![]() ��
��![]() ���߳�Ϊ
���߳�Ϊ![]() �������ΰ�ͼ
�������ΰ�ͼ![]() �ڷţ���ú���Ӱ��
�ڷţ���ú���Ӱ��![]() ��
��![]() �ij��Ⱥ�Ϊ
�ij��Ⱥ�Ϊ![]() ������������ľ��룮��д��������̣�����ú�
������������ľ��룮��д��������̣�����ú�![]() ��
��![]() ��
��![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�DZ߳�Ϊ3cm�ĵȱ������Σ���P��Q�ֱ�Ӷ���A��Bͬʱ���������߶�AB��BC�˶��������ǵ��ٶȶ�Ϊ1cm/s.����P�����Bʱ��P��Q����ֹͣ�˶�.���P���˶�ʱ��Ϊt��s����
��1����tΪ��ֵʱ����PBQ��ֱ�������Σ�
��2������AQ��CP���ཻ�ڵ�M�����P��Q���˶��Ĺ����У���CMQ��仯�����仯,��˵�����ɣ������䣬��������Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=nx2��3nx��4n��n��0����x�ύ��B��C���㣨��B�ڵ�C����ࣩ������������y�ύ�ڵ�A��
��1����B�������� ������C�������� ����
��2������BAC=90�����������ߵĽ���ʽ��
��3����M�ǣ�2�����������ϵĶ��㣬��N����Գ����ϵĶ��㣬�Ƿ���������ĵ�M��N��ʹ����A��C��M��NΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲���������������A��B����֮��ľ��룬����ʵ�������������ͼͼ�Σ�����AB��BE��EF��BE��AF��BE��D��C��BD�ϣ�����λͬѧ�ֱ�����������������ݣ���BC����ACB�� ��CD����ACB����ADB����EF��DE��BD����DE��DC��BC���ܸ����������ݣ����A��B���������� ��
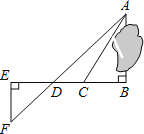
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com