
【题目】已知BD、CE分别是△ABC的AC边、AB边上的高,M是BC边的中点,分别连结MD、ME、DE。

(1)当∠BAC<90°时,垂足D、E分别落在边AC、AB上,如图1,求证:DM=EM;
(2)若∠BAC=120°,试判断△DEM的形状,并说明理由;
(3)当∠BAC= 时,△DEM是等腰直角三角形。
【答案】(1)见解析;(2)△DEM是等边三角形,理由见解析;(3)当∠BAC=135°时,△DEM是等腰直角三角形.
【解析】
(1)DM是Rt△BCD斜边BC上的中线,EM是Rt△BCE斜边BC上的中线,根据直角三角形斜边上的中线的性质进行证明即可;
(2)根据等腰三角形的性质得到∠DBM=∠BDM,∠MEC=∠MCE,由三角形的外角的性质得到∠BME =2∠MCE,∠CMD =2∠DBM,根据三角形的内角和得到∠DBM+∠MCE=60°,即可得到结论;
(3)设∠BAC=x,同(2)可推出∠DME=2x180°,当∠DME=90°时求出x即可.
(1)证明:∵BD、CE是△ABC的两条高,M是BC的中点,
∴在Rt△BDC中,MD是斜边BC上的中线,
∴DM=![]() BC;
BC;
同理,得EM=![]() BC,
BC,
∴DM=EM;
(2)如下图所示,∠BAC=120°,
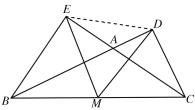
∵BM=CM=DM=EM,
∴∠DBM=∠BDM,∠MEC=∠MCE,
∴∠BME=∠MEC+∠MCE=2∠MCE,∠CMD=∠DBM+∠BDM =2∠DBM,
∵∠BAC=120°,
∴∠DBM+∠MCE=60°,
∴∠BME+∠CMD=2(∠MCE +∠DBM)=120°,
∴∠DME=60°,
又∵DM=EM
∴△DEM是等边三角形;
(3)∵BM=CM=DM=EM,
∴∠DBM=∠BDM,∠MEC=∠MCE,
∴∠BME=2∠MCE,∠CMD=2∠DBM,
设∠BAC=x,
∴∠DBC+∠MCE=180°x,
∴∠BME+∠CMD=360°2x,
∴∠DME=180°(∠BME+∠CMD)=2x180°,
当∠DME=90°时,△DEM是等腰直角三角形,
所以2x180°=90°,解得x=135°,
故当∠BAC=135°时,△DEM是等腰直角三角形


科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:△ABE≌△CAD;
(2)求∠BPQ的度数;
(3)求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 中,∠ABC=90°,AB=BC= ![]() ,三角形的顶点在相互平行的三条直线l1、l2、l3 上,且 l2、l3之间的距离为 2,则 l1、l2 之间的距离为______.
,三角形的顶点在相互平行的三条直线l1、l2、l3 上,且 l2、l3之间的距离为 2,则 l1、l2 之间的距离为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于![]() AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
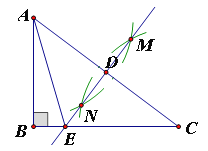
(1)∠ADE= °;
(2)AE CE(填“>、<、=”)
(3)当AB=3、AC=5时,△ABE的周长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BA=BC,BD是三角形的角平分线,DE∥BC交AB于E,下列结论:①∠1=∠3;②![]() ;③
;③![]() 。正确的有__________。(填序号)
。正确的有__________。(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,∠OAB=30°.
(Ⅰ)若点C在y轴上,且△ABC为以AB为腰的等腰三角形,求∠BCA的度数;
(Ⅱ)若B(1,0),沿AB将△ABO翻折至△ABD.请根据题意补全图形,并求点D的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】测量物体高度
![]() 小明想测量一棵树的高度
小明想测量一棵树的高度![]() ,在阳光下,小明测得一根长为
,在阳光下,小明测得一根长为![]() 米的竹竿的影长为
米的竹竿的影长为![]() 米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为
米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为![]() 米,落在地面上的影长为
米,落在地面上的影长为![]() 米,则树高
米,则树高![]() 为多少米.
为多少米.
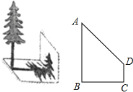
![]() 小明在某一时刻测得
小明在某一时刻测得![]() 的杆子在阳光下的影子长为
的杆子在阳光下的影子长为![]() ,他想测量电线杆
,他想测量电线杆![]() 的高度,但其影子恰好落在土坡的坡面
的高度,但其影子恰好落在土坡的坡面![]() 和地面
和地面![]() 上,量得
上,量得![]() ,
,![]() ,
,![]() 与地面成
与地面成![]() .
.
求电线杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋节是我国的传统节日,人们素有吃月饼的习俗.某超市在中秋节来临之际用3000元购进A、B两种月饼1100个,若购买A种月饼与购买B种月饼的费用相同,且A种月饼的单价是B种月饼单价的1.2倍.
(1)求A、B两种月饼的单价各是多少?
(2)若计划用不超过7000元的资金再次购进A、B两种月饼共2600个,已知A、B两种月饼的进价不变.求A种月饼最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE中,AB=AD=6,BC=DE,∠B=∠D=30°,边AD与边BC交于点P(不与点B,C重合),点B,E在AD异侧,I为△APC的内心.
(1)求证:∠BAD=∠CAE;
(2)设AP=x,请用含x的式子表示PD,并求PD的最大值;
(3)当AB⊥AC时,∠AIC的取值范围为m°<∠AIC<n°,分别直接写出m,n的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com