
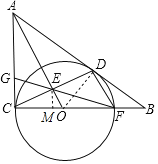
【题目】如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.

【答案】见解析
【解析】
(1)欲证明DF∥OA,只要证明OA⊥CD,DF⊥CD即可;
(2)过点作EM⊥OC于M,易知![]() ,只要求出EM、FM、FC即可解决问题;
,只要求出EM、FM、FC即可解决问题;
(1)证明:连接OD.
∵AB与⊙O相切与点D,又AC与⊙O相切与点,
∴AC=AD,∵OC=OD,
∴OA⊥CD,
∴CD⊥OA,
∵CF是直径,
∴∠CDF=90°,
∴DF⊥CD,
∴DF∥AO.
(2)过点作EM⊥OC于M,
∵AC=6,AB=10,
∴BC=![]() =8,
=8,
∴AD=AC=6,
∴BD=AB-AD=4,
∵BD2=BFBC,
∴BF=2,
∴CF=BC-BF=6.OC=![]() CF=3,
CF=3,
∴OA=![]() =3
=3![]() ,
,
∵OC2=OEOA,
∴OE=![]() ,
,
∵EM∥AC,
∴![]() ,
,
∴OM=![]() ,EM=
,EM=![]() ,FM=OF+OM=
,FM=OF+OM=![]() ,
,
∴![]() ,
,
∴CG=![]() EM=2.
EM=2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某加工企业生产并销售某种农产品,假设销售量与加工产量相等.已知每千克生产成本y1(单位:元)与产量x(单位:kg)之间满足表达式y1=![]() 下图中线段AB表示每千克销售价格y2(单位:元)与产量x(单位:kg)之间的函数表达式.
下图中线段AB表示每千克销售价格y2(单位:元)与产量x(单位:kg)之间的函数表达式.
(1)试确定每千克销售价格y2与产量x之间的函数表达式,并写出自变量的取值范围;
(2)若用w(单位:元)表示销售该农产品的利润,试确定w与产量x之间的函数表达式;
(3)求销售量为70 kg时,销售该农产品是赚钱,还是亏本?赚钱或亏本了多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为______.
周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形于1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示三角形的两条直角边(x>y),下列四个说法:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 。其中说法正确的是( )
。其中说法正确的是( )

A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于![]() AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
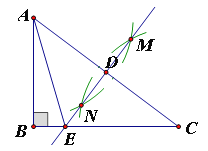
(1)∠ADE= °;
(2)AE CE(填“>、<、=”)
(3)当AB=3、AC=5时,△ABE的周长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:在综合与实践课上,同学们以“已知三角形三边的长度,求三角形面积”为主题开展数学活动,小颖想到借助正方形网格解决问题。图1、图2都是8×8的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点。
操作发现:小颖在图1中画出△ABC,其顶点A、B、C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE、EF分别经过点C、A,她借助此图求出了△ABC的面积。
(1)在图1中,小颖所画的△ABC的三边长分别是AB= ,BC= ,AC= ;△ABC的面积为 。
(2)请你根据小颖的思路,在图2中以格点为顶点画一个△DEF,使三角形三边长分别为2、![]() 、
、![]() ,并直接写出△DEF的面积= 。
,并直接写出△DEF的面积= 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,∠OAB=30°.
(Ⅰ)若点C在y轴上,且△ABC为以AB为腰的等腰三角形,求∠BCA的度数;
(Ⅱ)若B(1,0),沿AB将△ABO翻折至△ABD.请根据题意补全图形,并求点D的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD//BC,∠A=90°,E为AB上一点,且AE=BC,∠1=∠2.
请说明:(1)△ADE与△BEC全等吗?请说明理由;
(2)判断△CDE的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com