
【题目】先阅读下列解题过程,然后解答问题⑴、⑵,解方程:![]() 。
。
解:①当3x≥0时,原方程可化为一元一次方程3x=1,它的解是![]() ;
;
②当3x≤0时,原方程可化为一元一次方程-3x=1,它的解是![]() 。
。
⑴请你根据以上理解,解方程:![]() ;
;
⑵探究:当b为何值时,方程![]() ,①无解;②只有一个解;③有两个解。
,①无解;②只有一个解;③有两个解。
【答案】(1)![]() 或
或![]() ;(2)①
;(2)①![]() ;②
;②![]() ;③
;③![]() .
.
【解析】
(1)当x3≥0时,得出方程为2(x3)+5=13,求出方程的解即可;当x3<0时,得出方程为2(3x)+5=13,求出方程的解即可;
(2)根据绝对值具有非负性得出|x2|≥0,分别求出b+1<0,b+1=0,b+1>0的值,即可求出答案.
(1)解:当x3≥0时,
原方程可化为一元一次方程为2(x3)+5=13,
方程的解是x=7;
②当x3<0时,
原方程可化为一元一次方程为2(3x)+5=13,
方程的解是x=1.
(2)解:∵|x2|≥0,
∴当b+1<0,即b<1时,方程无解;
当b+1=0,即b=1时,方程只有一个解;
当b+1>0,即b>1时,方程有两个解.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式 | 直接销售 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 100 | 250 | 450 |
现在该公司收购了140吨蔬菜,已知该公司每天能精加工蔬菜6吨和粗加工蔬菜16吨(两种加工不能同时进行)。
(1)如果要求在18天内全部销售这140吨蔬菜,请完成下列表格:
销售方式 | 全部直接销售 | 全部粗加工后销售 | 尽量精加工,剩余部分直接销售 |
获利(元) |
(2)如果先进行精加工,来不及精加工的进行粗加工,要求15天内刚好加工完这140吨蔬菜,则应如何分配加工时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
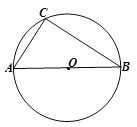
【题目】已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.
(1)求⊙O的半径;
(2)请用尺规作图作出点P,使得点P在优弧CAB上时,△PBC的面积最大,请保留作图痕迹,并求出△PBC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作一个以已知线段为对角线正方形”的尺规作图过程.
已知:线段AC
求证:四边形ABCD为正方形
作法:如图,
①作线段AC的垂直平分线MN 交AC于点O;
②以点O为圆心CO长为半径画圆,交直线MN于点B,D;
③顺次连接AB,BC,CD,DA;
所以四边形ABCD为所作正方形.

根据小明设计的尺规作图过程,完成以下任务.
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵OA=OB,OC=OD,
∴四边形 ABCD为平行四边形.(__________________)(填写推理依据)
∵OA=OB=OC=OD即AC=BD.
∴![]() ABCD为 (__________________)(填写推理依据).
ABCD为 (__________________)(填写推理依据).
∵ AC⊥BD,
∴四边形 ABCD为正方形(__________________________).(填写推理依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某公司有甲、乙两类经营收入,其中去年乙类收入为![]() 万元,去年甲类收入是乙类收入的2倍,预计今年甲类年收入减少9%,乙类收入将增加19%.今年该公司的年总收入比去年增加__________万元(用字母
万元,去年甲类收入是乙类收入的2倍,预计今年甲类年收入减少9%,乙类收入将增加19%.今年该公司的年总收入比去年增加__________万元(用字母![]() 来表示).
来表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y=![]() (x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为_____.
(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂加工齿轮,已知每1块金属原料可以加工成3个A齿轮或4个B齿轮(说明:每块金属原料无法同时既加工A齿轮又加B齿轮),已知1个A齿轮和2个B齿轮组成一个零件,为了加工更多的零件,要求A、B齿轮恰好配套.请列方程解决下列问题:
(1)现有25块相同的金属原料,问最多能加工多少个这样的零件?
(2)若把36块相同的金属原料全部加工完,问加工的A、B齿轮恰好配套吗?说明理由
(3)若把n块相同的金属原料全部加工完,为了使这样加工出来的A、B齿轮恰好配套,请求出n所满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,
(1)求弦AC的长;
(2)求证:BC∥PA.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在中俄“海上联合—2014”反潜演习中,我军舰A测得潜艇C的俯角为300.位于军舰A正上方1000米的反潜直升机B侧得潜艇C的俯角为680,试根据以上数据求出潜艇C离开海平面的下潜深度。(结果保留整数。参考数据:sin680≈0.9,cos680≈0.4,,tan680≈2.5. ![]() ≈1.7)
≈1.7)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com