
分析 (1)根据有理数的加减进行计算即可解答本题;
(2)根据幂的乘方、有理数的减法和乘法进行计算即可解答本题;
(3)根据幂的乘方、绝对值、有理数的乘除和加法进行计算即可解答本题.
解答 解:(1)0-(+8)+(-2.7)-(+5)
=0+(-8)+(-2.7)+(-5)
=-15.7;
(2)3-12012-($\frac{2}{3}$-$\frac{3}{5}$)×[4-(-$\frac{1}{2}$)2]
=3-1-$\frac{1}{15}×[4-\frac{1}{4}]$
=3-1-$\frac{1}{15}×\frac{15}{4}$
=3-1-$\frac{1}{4}$
=$\frac{7}{4}$;
(3)(-2)2+(-1-3)÷(-$\frac{2}{3}$)+|${-\frac{1}{16}}$|×(-24)
=4+(-4)×$(-\frac{3}{2})+\frac{1}{16}×(-16)$
=4+6-1
=9.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
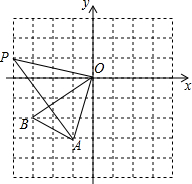 如图所示是由边长都为1的小正方形组成的8×8的正方形网格.若三角形的各个顶点郁在小正方形的顶点上.则这样的图形叫做格点三角形,已知△A0B是格点三角形.
如图所示是由边长都为1的小正方形组成的8×8的正方形网格.若三角形的各个顶点郁在小正方形的顶点上.则这样的图形叫做格点三角形,已知△A0B是格点三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
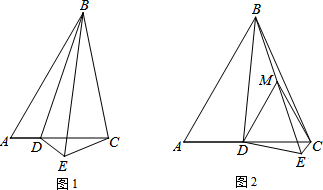
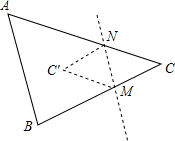 已知,如图,△ABC中,把点C沿直线MN对折得点C′.
已知,如图,△ABC中,把点C沿直线MN对折得点C′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
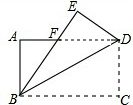 如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )
如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )| A. | $\frac{2}{5}$ | B. | $\frac{5}{13}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
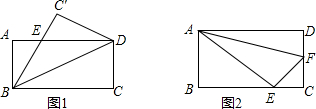
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com