
(本题满分10分)在平面直角坐标系中,点A的坐标为(-6, 6),以A为顶点的∠BAC的两边始终与x轴交于B、C两点(B在C左面),且∠BAC=45°.
(1)如图,连接OA,当AB=AC时,试说明:OA=OB.

(2)过点A作AD⊥x轴,垂足为D,当DC=2时,将∠BAC沿AC所在直线翻折,翻折后边AB交y轴于点M,求点M的坐标.


(1)见解析;(2)M点坐标为(0,3)或M点坐标为(0,—6).
【解析】
试题分析:(1)根据题目中角的度数,求出∠BAO=∠ABC=67.5°,利用等腰三角形的性质即可得出结论;
(2)根据题意,可知要分两种情况,即当点C在点D右侧时或当点C在点D左侧时,利用勾股定理即可得出M点坐标.
试题解析:
(1)∵AB=AC,∠BAC=45°,∴∠ABC=∠ACB= 67.5°.
过点A作AE⊥OB于E,则△AEO是等腰直角三角形,∠EAO=45°.
∵AB=AC,AE⊥OB,
∴∠BAE=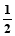 ∠BAC=22.5°.
∠BAC=22.5°.
∴∠BAO=67.5°=∠ABC
∴OA=OB,
(2)设OM=x.
当点C在点D右侧时,连接CM,过点A作AF⊥y轴于点F,
由∠BAM=∠DAF=90°可知:∠BAD=∠MAF;
∵AD=AF=6,∠BDA=∠MFA=90°,
∴△BAD≌△MAF.
∴BD=FM=6—x.
∵AC=AC,∠BAC=∠MAC,
∴△BAC≌△MAC.
∴BC=CM=8—x.
在Rt△COM中,由勾股定理得:OC2+OM2=CM2,即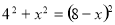 ,
,
解得:x=3,∴M点坐标为(0,3).
当点C在点D左侧时,连接CM,过点A作AF⊥y轴于点F,
同理,△BAD≌△MAF,∴BD=FM=6+x.
同理,△BAC≌△MAC,∴BC=CM=4+x.
在Rt△COM中,由勾股定理得:OC2+OM2=CM2,即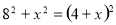 ,
,
解得:x=6,∴M点坐标为(0,—6)

考点:等腰三角形的性质;翻折的性质.


 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源:2014-2015学年重庆开县八年级上学期期末考试数学试卷(解析版) 题型:选择题
下列各式中,计算结果是x2+7x-18的是( )
A.(x-1)(x+18) B.(x+2)(x+9)
C.(x-3)(x+6) D.(x-2)(x+9)
查看答案和解析>>
科目:初中数学 来源: 题型:
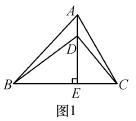
如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD、AC.
(1)试判断BD与AC的位置关系和数量关系,并说明理由.
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由.
(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变,
①试猜想BD与AC的数量关系,并说明理由.
②你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
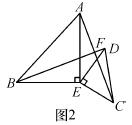
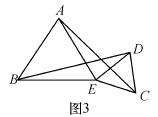
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校八年级上学期期末考试数学试卷(解析版) 题型:选择题
如果点P(m ,1-2m)在第一象限,那么m的取值范围是( )
A.0<m<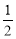 B.-
B.-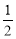 <m<0 C.m<0 D. m>
<m<0 C.m<0 D. m>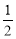
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期末调研考试数学试卷(解析版) 题型:解答题
(本题满分8分)如图,一次函数y=(m-1)x+3的图像与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为 .
.

(1)求m的值及点A的坐标;
(2)过点B作直线BP与x轴的正半轴相交于点P,且OP=2OA,求直线BP的函数表达式 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期末调研考试数学试卷(解析版) 题型:填空题
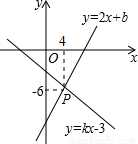
如图,已知函数y=2x+b与函数y=kx﹣3的图像交于点P,则不等式kx﹣3<2x+b的解集是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com