Question

【题目】△ABC中，三个内角的平分线交于点O，过点O作OD⊥OB，交边BC于点D．
（1）如图1，猜想∠AOC与∠ODC的关系，并说明你的理由；
（2）如图2，作∠ABC外角∠ABE的平分线交CO的延长线于点F． ①求证：BF∥OD；
②若∠F=35°，求∠BAC的度数．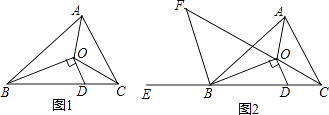

Answer 1

【答案】
（1）解：∠AOC=∠ODC，

理由：∵三个内角的平分线交于点O，

∴∠OAC+∠OCA= （∠BAC+∠BCA）= （180°﹣∠ABC），

∵∠OBC= ∠ABC，

∴∠AOC=180°﹣（∠OAC+∠OCA）=90°+ ∠ABC=90°+∠OBC，

∵OD⊥OB，

∴∠BOD=90°，

∴∠ODC=90°+∠OBD，

∴∠AOC=∠ODC

（2）解：①∵BF平分∠ABE，

∴∠EBF= ∠ABE= （180°﹣∠ABC）=90°﹣∠DBO，

∵∠ODB=90°﹣∠OBD，

∴∠FBE=∠ODB，

∴BF∥OD；

②∵BF平分∠ABE，

∴∠FBE= ∠ABE= （∠BAC+∠ACB），

∵三个内角的平分线交于点O，

∴∠FCB= ∠ACB，

∵∠F=∠FBE﹣∠BCF= （∠BAC+∠ACB）﹣ ∠ACB= ∠BAC，

∵∠F=35°，

∴∠BAC=2∠F=70°

【解析】（1）根据角平分线的定义得到∠OAC+∠OCA= （180°﹣∠ABC），∠OBC= ∠ABC，由三角形的内角和得到∠AOC=90°+∠OBC，∠ODC=90°+∠OBD，于是得到结论；（2）①由角平分线的性质得到∠EBF=90°﹣∠DBO，由三角形的内角和得到∠ODB=90°﹣∠OBD，于是得到结论；②由角平分线的性质得到∠FBE （∠BAC+∠ACB），∠FCB= ACB，根据三角形的外角的性质即可得到结论．
【考点精析】根据题目的已知条件，利用平行线的判定和三角形的内角和外角的相关知识可以得到问题的答案，需要掌握同位角相等，两直线平行;内错角相等，两直线平行;同旁内角互补，两直线平行；三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角．