
【题目】已知二次函数y=x2﹣2x﹣3与x轴交于A、B两点(A在B的左边),与y轴交于点C.
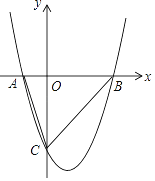
(1)求出点A、B、C的坐标.
(2)求S△ABC
(3)在抛物线上(除点C外),是否存在点N,使得S△NAB=S△ABC , 若存在,求出点N的坐标,若不 存在,请说明理由.
【答案】(1)A(﹣1,0)、B(3,0);(2)6;(3)存在,点N的坐标(1+ ![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)或(2,﹣3)
,3)或(2,﹣3)
【解析】试题分析:
(1)在解析式![]() 中,由
中,由![]() ,求得
,求得![]() 的对应值可得点C的坐标;由
的对应值可得点C的坐标;由![]() ,求得对应的
,求得对应的![]() 的值可得点A、B的坐标;
的值可得点A、B的坐标;
(2)根据(1)中所求点A、B、C坐标可求得△ABC的面积;
(3)设点N的纵坐标为![]() ,则由S△NAB=S△ABC可知
,则由S△NAB=S△ABC可知![]() 或
或![]() ,由点N在抛物线
,由点N在抛物线![]() 上,可得
上,可得![]() 或
或![]() ,解方程即可求得点N的横坐标,从而得到点N的坐标.
,解方程即可求得点N的横坐标,从而得到点N的坐标.
试题解析:
(1)在![]() 中,当
中,当![]() 时,
时,![]() ,
,
∴点C的坐标为:(0,﹣3),
当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,
∴点A的坐标为:(﹣1,0)、点B的坐标为:(3,0);
(2)∵点A的坐标为:(﹣1,0)、点B的坐标为:(3,0),
∴AB=3+1=4,
∵点C的坐标为:(0,﹣3),
∴OC=3,
∴S△ABC= ![]() ABOC=
ABOC=![]() ×4×3=6;
×4×3=6;
(3)存在点N,使S△NAB=S△ABC,
设点N的纵坐标为![]() ,
,
∵S△NAB=S△ABC,OC=3,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
解得:![]() 或
或![]() ,
,
∵点N不与点C重合,
∴点N的坐标为:(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)或(2,﹣3).
,3)或(2,﹣3).


科目:初中数学 来源: 题型:
【题目】越来越多的人在用微信付款、转账,把微信账户里的钱转到银行卡叫做提现。
自2016年3月l日起,每个微信账户终身享有1000元的免费提现额度,当累计提现金额超过1000元时,累计提现金额超出1000元的部分需支付0.1%的手续费,以后每次提现支付的手续费为提现金额的0.1%.
(1)小明在今天第1次进行了提现,金额为l600元,他需支付手续费_________元;
(2)小亮自2016年3月1日至今,用自己的微信账户共提现3次,3次提现金额和手续费分别如下:
第1次 | 第2次 | 第3次 | |
提现金额(元) | A | b |
|
手续费(元) | 0 | 0.4 | 3.4 |
问:小明3次提现金额各是多少元?
(3)单笔手续费小于0.1元的,按照0.1元收取(即提现不足100元,按照100元收取手续费).小红至今共提现两次,每次提现金额都是整数,共支付手续费2.4元,第一次提现900元。求小红第二次提现金额的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:现有![]() 个边长为
个边长为![]() 的正方形,排列形式如图
的正方形,排列形式如图![]() ,在图中画出分割线,拼出如图
,在图中画出分割线,拼出如图![]() 所示的新正方形.
所示的新正方形.

请你参考.上述做法,解决如下问题:
(1)现有![]() 个边长为
个边长为![]() 的正方形,排列形式如图
的正方形,排列形式如图![]() ,请把它们分割后拼接成一个新的正方形,在图
,请把它们分割后拼接成一个新的正方形,在图![]() 中画出分割线,并在图
中画出分割线,并在图![]() 的正方形网格中用实线画出拼接成的新正方形;(图中每个小正方形的边长均为
的正方形网格中用实线画出拼接成的新正方形;(图中每个小正方形的边长均为![]() )
)
(2)如图![]() ,现有由
,现有由![]() 个相同小正方形组成的十字形纸板,请在图中画出分割线,拼出一个新正方形.
个相同小正方形组成的十字形纸板,请在图中画出分割线,拼出一个新正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
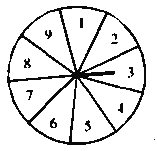
【题目】如图,一个均匀的转盘被平均分成9等份,分别标有1,2,3,4,5,6,7,8,9这9个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字.
小亮和小芳两人玩转盘游戏,对游戏规则,小芳提议:若转岀的数字是3的倍数,小芳获胜,若转出的数字是4的倍数,小亮获胜.
(1)你认为小芳的提议合理吗?为什么?
(2)利用这个转盘,请你为他俩设计一种对两人都公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果市场的甲、乙两家商店中都有批发某种水果,批发该种水果x千克时,在甲、乙两家商店所花的钱分别为y1元和y2元,已知y1、y2关于x的函数图象分别为如图所示的折线OAB和射线OC.

(1)当x的取值为 时,在甲乙两家店所花钱一样多?
(2)当x的取值为 时,在乙店批发比较便宜?
(3)如果批发30千克该水果时,在甲店批发比在乙店批发便宜50元,求射线AB的表达式,并写出定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交车每天的支出费用为60 元,每天的乘车人数 x(人)与每天利润(利润 =票款收入 -支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):
x(人) | … | 200 | 250 | 300 | 350 | 400 | … |
y(元) | … | -20 | -10 | 0 | 10 | 20 | … |
根据表格中的数据,回答下列问题:
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为 5 00人时,利润是多少?
(4) 试写出该公交车每天利润 y(元)与每天乘车人数x (人)的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图①,AC是菱形ABCD的对角线,∠B=60°,E、F分别是边BC、CD上的中点,连结AE、EF、AF.若AC=2,则CE+CF的长为_____.
(探究)如图②,在菱形ABCD中,∠B=60°.E是边BC上的点,连结AE,作∠EAF=60°,边AF交边CD于点F,连结EF.若BC=2,求CE+CF的长.
(应用)在菱形ABCD中,∠B=60°.E是边BC延长线上的点,连结AE,作∠EAF=60°,边AF交边CD延长线于点F,连结EF.若BC=2,EF⊥BC时,借助图③直接写出△AEF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′ ,如图①所示,∠BAB′ =θ, ![]() ,我们将这种变换记为[θ,n] .
,我们将这种变换记为[θ,n] .
(1)如图①,对△ABC作变换[60°,![]() ]得到△AB′C′ ,则
]得到△AB′C′ ,则![]() :
:![]() = ;直线BC与直线B′C′所夹的锐角为 度;
= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、![]() 在同一直线上,且四边形ABB′C′为矩形,求θ和n的值;
在同一直线上,且四边形ABB′C′为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com