练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】请阅读下列材料：

    问题：现有个边长为的正方形，排列形式如图，在图中画出分割线，拼出如图所示的新正方形．

    请你参考．上述做法，解决如下问题：

    （1）现有个边长为的正方形，排列形式如图，请把它们分割后拼接成一个新的正方形，在图中画出分割线，并在图的正方形网格中用实线画出拼接成的新正方形；（图中每个小正方形的边长均为）

    （2）如图，现有由个相同小正方形组成的十字形纸板，请在图中画出分割线，拼出一个新正方形．

    【答案】（1）见解析；（2）见解析

    【解析】

    （1）根据面积为10的正方形的边长为，可得三个并列的小正方形的对角线的长为；

    （2）根据面积为8的正方形的边长为，可得三个并列的小正方形的对角线的长为.

    （1）如图所示即为所求.

    （2）如图所示即为所求.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，是的中点，以为直径的⊙交的边于点、、.

    (1)求证:四边形是平行四边形;

    (2)若，求的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知四边形ABCD为正方形，AB=2，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE，EF为邻边作矩形DEFG，连接CG．

    （1）求证：矩形DEFG是正方形；

    （2）探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由；

    （3）设AE=x，四边形DEFG的面积为S，求出S与x的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

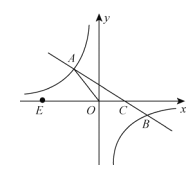
    【题目】如图，在平面直角坐标系xoy中，一次函数y=kx+b（k≠0）的图象与反比例函数（m≠0）的图象交于二、四象限内的A、B两点，与x轴交于C点，点B的坐标为（6，n）。线段OA=5，E为x轴上一点，且.

    (1)求该反比例函数和一次函数的解析式；

    (2)求△AOC的面积；

    (3)直接写出一次函数值大于反比例函数自变量x的取值范围。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲口袋中放有3个红球和5个白球，乙口袋中放有7个红球和9个白球，所有球除颜色外都相同．充分搅匀两个口袋，分别从两个口袋中任意摸出一个球，设从甲中摸出红球的概率是(红)，从乙中摸出红球的概率是(红)．

    (1)求(红)与(红)的值，并比较它们的大小．

    (2)将甲、乙两个口袋的球都倒入丙口袋，充分搅匀后，设从丙中任意摸出一球是红球的概率为(红)．小明认为：(红)(红)(红)．他的想法正确吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公交车每天的支出费用为600元，每天的乘车人数x（人）与每天利润（利润＝票款收入﹣支出费用）y（元）的变化关系如下表所示（每位乘客的乘车票价固定不变）：

    x（人）

    …

    200

    250

    300

    350

    400

    …

    Y（元）

    …

    ﹣200

    ﹣100

    0

    100

    200

    …

    根据表格中的数据，回答下列问题：

    （1）在这个变化关系中，自变量是什么？因变量是什么？

    （2）若要不亏本，该公交车每天乘客人数至少达到多少？

    （3）请你判断一天乘客人数为500人时，利润是多少？

    （4）试写出该公交车每天利润y（元）与每天乘车人数x（人）的关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=x2﹣2x﹣3与x轴交于A、B两点（A在B的左边），与y轴交于点C．

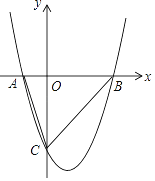
    （1）求出点A、B、C的坐标．

    （2）求S△ABC

    （3）在抛物线上（除点C外），是否存在点N，使得S△NAB=S△ABC ， 若存在，求出点N的坐标，若不 存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在菱形中，，，点是上一点，点在上，且，设．

    （1）当时，如图2，求的长；

    （2）设，求关于的函数关系式及其定义域；

    （3）若是以为腰的等腰三角形，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（﹣3，y1）、点B（﹣，y2）、点C（，y3）在该函数图象上，则y1＜y3＜y2；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x1和x2，且x1＜x2，则x1＜﹣1＜5＜x2．其中正确的结论有（　　）

    A. 2个 B. 3个 C. 4个 D. 5个

    查看答案和解析>>

    同步练习册答案