
【题目】如图1,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,点
上一点,点![]() 在
在![]() 上,且
上,且![]() ,设
,设![]() .
.

(1)当![]() 时,如图2,求
时,如图2,求![]() 的长;
的长;

(2)设![]() ,求
,求![]() 关于
关于![]() 的函数关系式及其定义域;
的函数关系式及其定义域;
(3)若![]() 是以
是以![]() 为腰的等腰三角形,求
为腰的等腰三角形,求![]() 的长.
的长.
【答案】(1)![]() =
=![]() (2)y=
(2)y=![]() x-8(
x-8(![]() ≤x≤
≤x≤![]() )(3)4
)(3)4![]()
【解析】
(1)先根据菱形的边长和对角线的长得到∠ABO =30°,再根据![]() ,求出AP的长,故可得到DP的长;
,求出AP的长,故可得到DP的长;
(2)作HP⊥AB,根据AP=PQ,得到AH=QH=![]() ,BH=8-
,BH=8-![]() ,BP=BD-DP=
,BP=BD-DP=![]() -x,再根据(1)可得HP=
-x,再根据(1)可得HP=![]() -
-![]() x,在Rt△BPH中,BP2=HB2+HP2,化简即可求解,再求出x的取值范围;
x,在Rt△BPH中,BP2=HB2+HP2,化简即可求解,再求出x的取值范围;
(3)根据题意作图,由等腰三角形的性质可得△AQP是等边三角形,故可得到DP的长.
(1)∵![]() ,
,![]() ,
,
∴BO=![]() =4
=4![]() ,AC⊥BD
,AC⊥BD
故AO=![]() =4=
=4=![]()
∴∠ABO =30°=∠ADO
∵![]()
∴∠APB =90°-∠ABO =60°
故∠PAD=∠APB -∠ADO =30°
即∠PAD=∠ADO
∴DP=AP
设AP=x,则BP=2x,
在Rt△ABP中,BP2=AB2+AP2
即(2x)2=82+x2
解得x=![]()
故![]() =
=![]() ;
;
(2)作HP⊥AB,∵AP=PQ
∴AH=QH=![]()
∴BH=BQ+QH=(8-y)+![]() =8-
=8-![]() ,
,
BP=BD-DP=![]() -x,
-x,
由(1)可得HP=![]() =
=![]() -
-![]() x
x
在Rt△BPH中,BP2=HB2+HP2
即(![]() -x)2=(8-
-x)2=(8-![]() )2+(
)2+(![]() -
-![]() x)2
x)2
∵![]() -x>0,8-
-x>0,8-![]() >0,
>0,![]() -
-![]() x>0
x>0
∴化简得y=![]() x-8
x-8
∵0≤![]() x-8≤8
x-8≤8
∴x的取值范围为![]() ≤x≤
≤x≤![]()
∴![]() 关于
关于![]() 的函数关系式是y=
的函数关系式是y=![]() x-8(
x-8(![]() ≤x≤
≤x≤![]() );
);
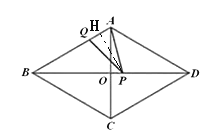
(3)如图,若![]() 是以
是以![]() 为腰的等腰三角形,
为腰的等腰三角形,
则∠QPB=∠QBP=30°,
∴∠AQP=∠QPB+∠QBP=60°
∵∠BAP=90°-∠QBP=60°,
∴△APQ是等边三角形,∠APQ=60°
∴∠QPB +∠APQ=90°,
则AP⊥BP,故O点与P点重合,
∴PD=DO=![]() =4
=4![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】两个反比例函数y=![]() (k>1)和y=
(k>1)和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y=![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=![]() 的图象于点B,BE⊥x轴于点E,当点P在y=
的图象于点B,BE⊥x轴于点E,当点P在y=![]() 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)
图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:现有![]() 个边长为
个边长为![]() 的正方形,排列形式如图
的正方形,排列形式如图![]() ,在图中画出分割线,拼出如图
,在图中画出分割线,拼出如图![]() 所示的新正方形.
所示的新正方形.

请你参考.上述做法,解决如下问题:
(1)现有![]() 个边长为
个边长为![]() 的正方形,排列形式如图
的正方形,排列形式如图![]() ,请把它们分割后拼接成一个新的正方形,在图
,请把它们分割后拼接成一个新的正方形,在图![]() 中画出分割线,并在图
中画出分割线,并在图![]() 的正方形网格中用实线画出拼接成的新正方形;(图中每个小正方形的边长均为
的正方形网格中用实线画出拼接成的新正方形;(图中每个小正方形的边长均为![]() )
)
(2)如图![]() ,现有由
,现有由![]() 个相同小正方形组成的十字形纸板,请在图中画出分割线,拼出一个新正方形.
个相同小正方形组成的十字形纸板,请在图中画出分割线,拼出一个新正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果市场的甲、乙两家商店中都有批发某种水果,批发该种水果x千克时,在甲、乙两家商店所花的钱分别为y1元和y2元,已知y1、y2关于x的函数图象分别为如图所示的折线OAB和射线OC.

(1)当x的取值为 时,在甲乙两家店所花钱一样多?
(2)当x的取值为 时,在乙店批发比较便宜?
(3)如果批发30千克该水果时,在甲店批发比在乙店批发便宜50元,求射线AB的表达式,并写出定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交车每天的支出费用为60 元,每天的乘车人数 x(人)与每天利润(利润 =票款收入 -支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):
x(人) | … | 200 | 250 | 300 | 350 | 400 | … |
y(元) | … | -20 | -10 | 0 | 10 | 20 | … |
根据表格中的数据,回答下列问题:
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为 5 00人时,利润是多少?
(4) 试写出该公交车每天利润 y(元)与每天乘车人数x (人)的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的![]() 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这![]() 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图①,AC是菱形ABCD的对角线,∠B=60°,E、F分别是边BC、CD上的中点,连结AE、EF、AF.若AC=2,则CE+CF的长为_____.
(探究)如图②,在菱形ABCD中,∠B=60°.E是边BC上的点,连结AE,作∠EAF=60°,边AF交边CD于点F,连结EF.若BC=2,求CE+CF的长.
(应用)在菱形ABCD中,∠B=60°.E是边BC延长线上的点,连结AE,作∠EAF=60°,边AF交边CD延长线于点F,连结EF.若BC=2,EF⊥BC时,借助图③直接写出△AEF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
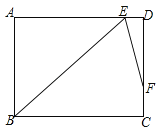
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5 000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5 000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为284万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com